How to convert FA to Left Linear Grammar in TOC?

A grammar with at most one variable at the right side of production is called linear grammar.

Following is an example of the linear grammar −

S→aSb/ε

Here, if you observe, we can write the same production by dividing …..

S→Ab

A→aAb

A→ε

Left Linear Grammar

A grammar is left linear grammar where all non-terminals in the right hand sides are at the left end.

For example,

A→Sa/ε

Steps for conversion

The steps for the conversion of finite automata (FA) to the left linear grammar are as follows −

Step 1 − Take reverse of the finite automata

Step 2 − write right linear grammar

Step 3 − Then take reverse of the right linear grammar

Step 4 − And finally, you will get left linear grammar

Consider a Finite Automata as given below −

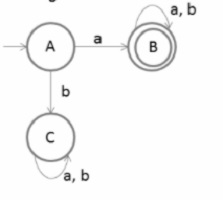
Make final state as initial state and initial state as final state, as shown below −

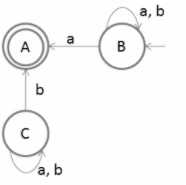
Now remove the unreachable states, as shown below −

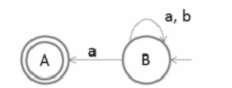
After removing the unreachable states, the transition diagram is not in the deterministic finite automata (DFA) because state A has no output symbol whereas state B is having two outputs on symbol ‘a’

So the resultant diagram looks like the Non-deterministic finite automata (NFA).

First, generate the right linear grammar for the final transition diagram −

      B→aA/aB/bB

      A→ε

Now reverse the right linear grammar to generate left linear grammar −

      B → Ba/Bb/Aa

      A→ε