Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Inductive Hypothesis in TOC?
Induction is a powerful tool in mathematics. It is a way of proving propositions that hold for all natural numbers.
Hypothesis − The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order to prove the first or initial statement. The initial statement is called Hypothesis.
Suppose there exists a k > 0 such that for any regular expression r where 0 < OP(r) < k, there exists an NFA- s such that L(M) = L(r). Furthermore, suppose that M has exactly one final state.
Inductive Step
Let r be a regular expression with k + 1 operators (OP(r) = k + 1), where k + 1 >= 1.
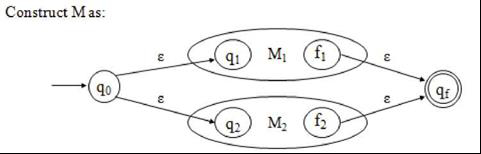
Case 1 − r = ri + r2
Since OP(r) = k +1, it follows that 0<= OP(n), OP(r2) <= k. By the inductive hypothesis, there exist Non-deterministic finite automata (NFA-s) machines M1 and M2 such that L(Mt) = L(n) and L(M) = L(r2).
Furthermore, both M1 and M2 have exactly one final state. We can construct M as given below −
Case 2 − r = r1r2
Since OP(r) = k+1, it follows that 0<= OP(r1), OP(r2) <= k. By the inductive hypothesis, there exist NFA-s machines M1 and M2 such that L(M1) = L(n) and L(M2) = L(r2).
Furthermore, both M1 and M2 have exactly one final state. We can now construct M as given below −
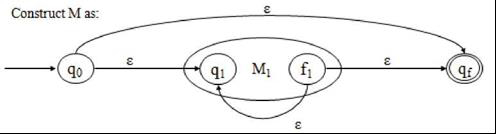
Case 3 − r = ri*
Since OP(r) = k+1, it follows that 0<= OP(ri) <= k. By the inductive hypothesis, there exists an NFA-s machine M1 such that L(M1) = L(n).
Furthermore, M1 has exactly one final state. Hence, we can construct M as follows −
1K+ Views
