
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain Operator grammar and precedence parser in TOC
If the grammar satisfies the following two conditions, then we can say that type of grammar is called as operator precedence grammar.
If ε is on its RHS then there exists no production rule.
If two non-terminals are adjacent to each other on its RHS then there exists no production rule.
Operator Grammars have the property that no production right side is empty or has two adjacent non-terminals.
Example
E-> E A E | id
A-> + | *
The above grammar is not an operator grammar but we can convert that grammar into operator grammar like −
E-> E + E | E * E | id
There are three precedence relations, which are given below −
| Relation |
Meaning |
|---|---|
|
a ? b |
a yields precedence to b |
|
a = · b |
a has the same precedence as b |
|
a ? b |
atakes precedence over b |
Precedence Table
| id |
+ |
* |
$ |
|
|---|---|---|---|---|
| id |
? |
? |
? |
|
| + |
? |
? |
? |
? |
| * |
? |
? |
? |
? |
| $ |
? |
? |
? |
? |
Precedencce Table
Example
The input string is as follows −
id1 + id2 * id3
After inserting precedence relations is−
$ <· id1 ·> + <· id2 ·> * <· id3 ·> $
Basic Principle
Scan the string from left until seeing ·> and put a pointer.
Scan backwards the string from right to left until seeing <·
Everything between the two relations <· and ·> forms the handle.
Replace handle with the head of the production.
Operator Precedence Parsing Algorithm
The algorithm is as follows −
Initialize: Set P to point to the first symbol of the input string w$
Repeat − Let b be the top stack symbol, a is the input symbol pointed to by P.
if (a is $ and b is $)
return
else
if a ·> b or a =· b then
push a onto the stack
advance P to the next input symbol
else if a <· b then
repeat
c -> pop the stack
until (c .> stack-top)
else error
end
Example
| id |
+ |
* |
$ |
|
|---|---|---|---|---|
| id |
? |
? |
? |
|
| + |
? |
? |
? |
? |
| * |
? |
? |
? |
? |
| $ |
? |
? |
? |
? |
Construct a graph using the algorithm. This graph is as follows −
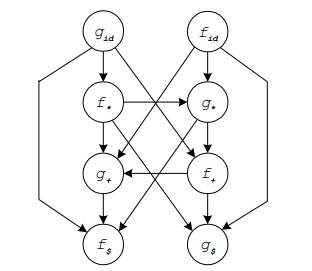
By seeing this, we can extract the precedence function like −
| id |
+ |
* |
$ |
|
|---|---|---|---|---|
| f |
4 |
2 |
4 |
0 |
| g |
5 |
1 |
3 |
0 |

