Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Power Factor and Power Triangle?
Power Factor
The cosine of angle between voltage and current in an AC circuit is called the power factor of the circuit. In other words, the power factor is defined as the ratio of active power to the apparent power in the circuit, i.e.,
$$\mathrm{\mathrm{Power\: factor,}\:\mathrm{cos}\:\phi \:=\:\frac{\mathrm{Active\: power\: (in\: Watts)}}{\mathrm{Apparent\: power \:(in\: VA)}}}$$
Where,$\phi$ is the power factor angle.
In an AC circuit, there may be a phase difference ($\phi$) between voltage and current. The term cos $\phi$ is called the power factor of the circuit.
When the given circuit is inductive, then the current lags behind the voltage and the power factor is termed as lagging power factor.
When the given circuit is capacitive, the current leads the voltage and hence the power factor of the circuit is referred to as leading power factor.
Consider an inductive circuit drawing a lagging current I at a supply voltage of V volts. The angle of lag being $\phi$. The phasor diagram of the circuit is shown in Figure-1.
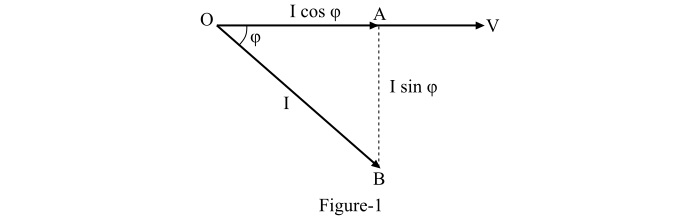
As the total circuit current I can be resolved into two perpendicular components as −
$$\mathrm{\mathrm{Current\: in\: phase \:with}\:\mathit{V}\:=\:\mathit{I}\:\mathrm{cos}\:\phi }$$
$$\mathrm{\mathrm{Current\: perpendicular \:to}\:\mathit{V}\:=\:\mathit{I}\:\mathrm{sin}\:\phi}$$
Here, the component ($I\:\mathrm{cos}\:\phi$) is called the active component while the component ($I\:\mathrm{sin}\:\phi$) is called the reactive component. The reactive component of the circuit current is the measure of power factor, i.e., if the reactive component is small, the power factor of the circuit will be high and vice-versa. The power factor of a circuit can never be more than unity.
Power Triangle
The power factor of an AC circuit can also be analysed in terms of power drawn by the circuit. If each side of the current triangle of Figure-1 is multiplied by the voltage V, the resulting triangle is called the power triangle of the circuit as shown in Figure-2.
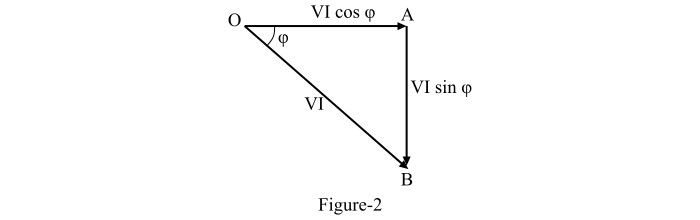
From the power triangle,
The active power component in Watts or kW is,
$$\mathrm{\mathrm{OA}\:=\:\mathit{VI}\:\mathrm{cos}\phi}$$
The reactive power component in VAR or kVAR is,
$$\mathrm{\mathrm{AB}\:=\:\mathit{VI}\:\mathrm{sin}\phi }$$
The apparent power in VA or kVA is,
$$\mathrm{\mathrm{OB}\:=\:\mathit{VI}}$$
The important points observed from the power triangle are as follows −
The total power or apparent power in an AC circuit is expressed as −
$$\mathrm{\mathrm{OB^{\mathrm{2}}}\:=\:\mathrm{OA^{\mathrm{2}}}\:+\:\mathrm{AB^{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow \mathrm{\left ( kVA \right )^{\mathrm{2}}}\:=\:\mathrm{\left ( kW \right )^{\mathrm{2}}}\:+\:\mathrm{\left ( kVAR \right )^{\mathrm{2}}}}$$
The power factor of the circuit is given by,
$$\mathrm{\mathrm{cos}\phi \:=\:\frac{\mathrm{OA}}{\mathrm{OB}}\:=\:\frac{\mathrm{kW}}{\mathrm{kVA}}}$$
i.e., the power factor of the circuit is the ratio of active power to the apparent power.
The lagging reactive power is responsible for the low power factor of the circuit. From the power triangle, it can be observed that smaller the reactive power component, the larger is the power factor of the circuit and vice-versa, i.e.,
$$\mathrm{\mathrm{kVAR}\:=\:\mathrm{kVA}\:\times \mathrm{sin}\:\phi \:=\:\frac{\mathrm{kW}}{\mathrm{cos}\:\phi}\:\times \:\mathrm{sin}\:\phi}$$
From the power triangle, the power factor of a circuit can be defined in one of the following ways −
$$\mathrm{\mathrm{Power\: factor}\:=\:\mathrm{cos}\:\phi }$$
Or,
$$\mathrm{\mathrm{Power\: factor}\:=\:\frac{\mathrm{Resistance}}{\mathrm{Impedance}}\:=\:\frac{\mathit{R}}{\mathit{Z}}}$$
Or,
$$\mathrm{\mathrm{Power\: factor}\:=\:\frac{\mathrm{Active\: power}}{\mathrm{Apparent \:power}}\:=\:\frac{\mathit{VI}\:\mathrm{cos}\:\phi }{\mathit{VI}}}$$
The reactive power be neither consumed in the circuit nor it does any useful work. It only flows back and forth in both directions in the circuit.
3K+ Views
To Continue Learning Please Login