Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Electric Power?
Electric Power: Definition
The rate at which work is done in an electric circuit is known as electric power. In other words, the energy used per unit time in an electric circuit is called as electric power.
Electric Power: Formula
As, the electric power is the rate of doing work in an electric circuit, thus,
$$\mathrm{Electric\:power,P=\frac{Work\:done\:in\:elecric\:circuit(W)}{Time(t)}}$$
Consider an electric circuit shown below. An electric current flows in the circuit, when a voltage is applied to it. So, work is being done in moving the charge (electrons) in the circuit. This work done in moving the charge per unit time is known as electric power.
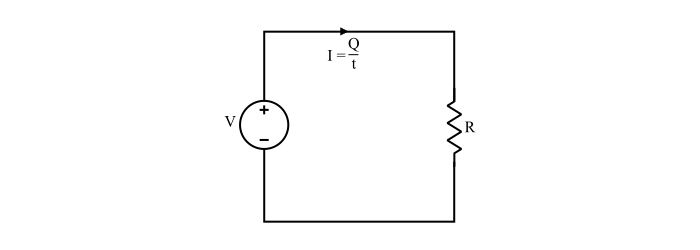
As the voltage is defined as the work done on the charge, i.e.
\mathrm{$$V=\frac{Work\:done}{Q}}$$
$$\mathrm{\Rightarrow\:{Work\:done},W=VQ=Vlt\:\:\:\:(\because\:Q=It)}$$
∴ Electric power,
$$\mathrm{P=\frac{Work\:done(W)}{t}=\frac{VQ}{t}=\frac{Vlt}{t}=VI\:\:\:\:\:\:Joule/sec\:or\:Watt}$$
$$\mathrm{(\because\:V=IR\:\:or\:\:I=\frac{V}{cR})}$$
$$\mathrm{\therefore\:P=VI=I^{2}R=\frac{V^{2}}{R}\:\:\:\:...(1)}$$
Equation (1) gives the three formulae for the calculation of electric power which are equally valid in a DC circuit.
Unit of Electric Power
The electric power in an electric circuit is measured in Watts (W). There some larger units are also for the power measurement as follows −
Kilowatt (kW) = 1000 Watts = 103 Watts
Megawatt (MW) = 103 kW = 106 W
Gigawatt (GW) = 109 W.
Numerical Example (1)
A resistor of 100 Ω has a DC voltage of 120 V across it. Calculate the power absorbed.
Solution −
Power absorbed,
$$\mathrm{P=\frac{V^{2}}{R}=\frac{120^{2}}{100}=144\:W}$$
Numerical Example (2)
If a current of 10 A flows through a resistor of 250Ω, determine the power dissipated in the resistor.
Solution −
Power Dissipated,
$$\mathrm{P=I^{2}R}$$
$$\mathrm{=10^{2}\times\:250}$$
$$\mathrm{=25000\:W=25\:kW}$$
Numerical Example (3)
A resistor of resistance R is connected across a dc supply of 12 V. The electric power dissipated is 6 Watt. Determine the value of R in Ohms.
Solution −
$$\mathrm{Electric\:power,P=\frac{V^{2}}{R}}$$
$$\mathrm{\Rightarrow\:R=\frac{V^{2}}{P}=\frac{12^{2}}{6}=24\:\Omega}$$
370 Views
