Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Understanding Logistic Regression in Python?
Logistic Regression is a statistical technique to predict the binary outcome. It’s not a new thing as it is currently being applied in areas ranging from finance to medicine to criminology and other social sciences.
In this section we are going to develop logistic regression using python, though you can implement same using other languages like R.
Installation
We’re going to use below libraries in our example program,
Numpy: To define the numerical array and matrix
Pandas: To handle and operate on data
Statsmodels: To handle parameter estimation & statistical testing
Pylab: To generate plots
You can install above libraries using pip by running below command in CLI.
>pip install numpy pandas statsmodels
Example Use case for Logistic Regression
To test our logistic regression in python, we are going to use the logit regression data provided by UCLA (Institute for digital research and education). You can access the data from below link in csv format: https://stats.idre.ucla.edu/stat/data/binary.csv
I have saved this csv file in my local machine & will read the data from there, you can do either. With this csv file we are going to identify the various factors that may influence admission into graduate school.
Import required libraries & load dataset
We are going to read the data using pandas library (pandas.read_csv):
import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np
df = pd.read_csv('binary.csv')
#We can read the data directly from the link \
# df = pd.read_csv(‘https://stats.idre.ucla.edu/stat/data/binary.csv’)
print(df.head())Output
admit gre gpa rank 0 0 380 3.61 3 1 1 660 3.67 3 2 1 800 4.00 1 3 1 640 3.19 4 4 0 520 2.93 4
As we can see from above output, one column name is ‘rank’, this may create problem since ‘rank’ is also name of the method in pandas dataframe. To avoid any conflict, i’m changing the name of rank column to ‘prestige’. So let’s change the dataset column name:
df.columns = ["admit", "gre", "gpa", "prestige"] print(df.columns)
Output
Index(['admit', 'gre', 'gpa', 'prestige'], dtype='object') In [ ]:
Now everything looks ok, we can now look much deeper what our dataset contains.
#Summarise the data
Using pandas function describe we’ll get a summarized view of everything.
print(df.describe())
Output
admit gre gpa prestige count 400.000000 400.000000 400.000000 400.00000 mean 0.317500 587.700000 3.389900 2.48500 std 0.466087 115.516536 0.380567 0.94446 min 0.000000 220.000000 2.260000 1.00000 25% 0.000000 520.000000 3.130000 2.00000 50% 0.000000 580.000000 3.395000 2.00000 75% 1.000000 660.000000 3.670000 3.00000 max 1.000000 800.000000 4.000000 4.00000
We can get the standard deviation of each column of our data & the frequency table cutting prestige and whether or not someone was admitted.
# take a look at the standard deviation of each column print(df.std())
Output
admit 0.466087 gre 115.516536 gpa 0.380567 prestige 0.944460 dtype: float64
Example
# frequency table cutting presitge and whether or not someone was admitted print(pd.crosstab(df['admit'], df['prestige'], rownames = ['admit']))
Output
prestige 1 2 3 4 admit 0 28 97 93 55 1 33 54 28 12
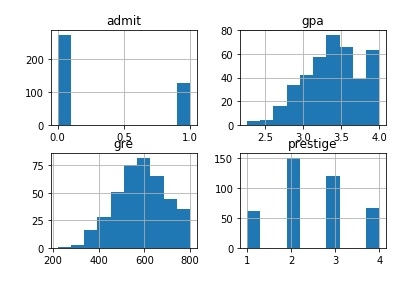
Let’s plot all the columns of the dataset.
# plot all of the columns df.hist() pl.show()
Output
Dummy Variables
Python pandas library provides great flexibility in how we categorical variables are represented.
# dummify rank dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige') print(dummy_ranks.head())
Output
prestige_1 prestige_2 prestige_3 prestige_4 0 0 0 1 0 1 0 0 1 0 2 1 0 0 0 3 0 0 0 1 4 0 0 0 1
Example
# create a clean data frame for the regression cols_to_keep = ['admit', 'gre', 'gpa'] data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':])
Output
admit gre gpa prestige_2 prestige_3 prestige_4 0 0 380 3.61 0 1 0 1 1 660 3.67 0 1 0 2 1 800 4.00 0 0 0 3 1 640 3.19 0 0 1 4 0 520 2.93 0 0 1 In [ ]:
Performing the regression
Now we are going to do logistic regression, which is quite simple. We simply specify the column containing the variable we’re trying to predict followed by the columns that the model should use to make the prediction.
Now we are predicting the admit column based on gre, gpa and prestige dummy variables prestige_2, prestige_3 & prestige_4.
train_cols = data.columns[1:] # Index([gre, gpa, prestige_2, prestige_3, prestige_4], dtype=object) logit = sm.Logit(data['admit'], data[train_cols]) # fit the model result = logit.fit()
Output
Optimization terminated successfully. Current function value: 0.573147 Iterations 6
Interpreting the Result
Let’s generate the summary output using statsmodels.
print(result.summary2())
Output
Results: Logit =============================================================== Model: Logit No. Iterations: 6.0000 Dependent Variable: admit Pseudo R-squared: 0.083 Date: 2019-03-03 14:16 AIC: 470.5175 No. Observations: 400 BIC: 494.4663 Df Model: 5 Log-Likelihood: -229.26 Df Residuals: 394 LL-Null: -249.99 Converged: 1.0000 Scale: 1.0000 ---------------------------------------------------------------- Coef. Std.Err. z P>|z| [0.025 0.975] ---------------------------------------------------------------- gre 0.0023 0.0011 2.0699 0.0385 0.0001 0.0044 gpa 0.8040 0.3318 2.4231 0.0154 0.1537 1.4544 prestige_2 -0.6754 0.3165 -2.1342 0.0328 -1.2958 -0.0551 prestige_3 -1.3402 0.3453 -3.8812 0.0001 -2.0170 -0.6634 prestige_4 -1.5515 0.4178 -3.7131 0.0002 -2.3704 -0.7325 intercept -3.9900 1.1400 -3.5001 0.0005 -6.2242 -1.7557 ==============================================================
The above result object also lets us to isolate and inspect parts of the model output.
#look at the confidence interval of each coeffecient print(result.conf_int())
Output
0 1 gre 0.000120 0.004409 gpa 0.153684 1.454391 prestige_2 -1.295751 -0.055135 prestige_3 -2.016992 -0.663416 prestige_4 -2.370399 -0.732529 intercept -6.224242 -1.755716
From above output, we can see there is an inverse relationship b/w the probability of being admitted and the prestige of a candidate’s undergraduate school.
So the probability of a candidate to being accepted into a graduate program is higher for students who attended a top ranked undergraduate college(prestige_1= True) as opposed to a lower ranked school (prestige_3 or prestige_4).
231 Views
