
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Identifying handwritten digits using Logistic Regression in PyTorch?
In this we are going to use PyTorch to train a CNN to recognize handwritten digit classifier using the MNIST dataset.
MNIST is a widely used dataset for hand-written classification task covering more than 70k labeled 28*28 pixel grayscale images of handwritten digits. The dataset contains almost 60k training images and 10k test images. Our job is to train a model using 60k training images and subsequently test its classification accuracy on 10k test images.
Installation
First we need the MXNet latest version, for that just run the following on your terminal:
$pip install mxnet
And you will something like,
Collecting mxnet Downloading https://files.pythonhosted.org/packages/60/6f/071f9ef51467f9f6cd35d1ad87156a29314033bbf78ad862a338b9eaf2e6/mxnet-1.2.0-py2.py3-none-win32.whl (12.8MB) 100% |????????????????????????????????| 12.8MB 131kB/s Requirement already satisfied: numpy in c:\python\python361\lib\site-packages (from mxnet) (1.16.0) Collecting graphviz (from mxnet) Downloading https://files.pythonhosted.org/packages/1f/e2/ef2581b5b86625657afd32030f90cf2717456c1d2b711ba074bf007c0f1a/graphviz-0.10.1-py2.py3-none-any.whl …. …. Installing collected packages: graphviz, mxnet Successfully installed graphviz-0.10.1 mxnet-1.2.0
Second, we need the torch & torchvision library- if it’s not where you can install it using pip.
Import Library
import torch import torchvision
Load the MNIST dataset
Before we start working on our program, we need the MNIST dataset. So lets loads the images and labels into memory and define the hyperparameters we’ll be using for this experiment.
#n_epochs are the number of times, we'll loop over the complete training dataset n_epochs = 3 batch_size_train = 64 batch_size_test = 1000 #Learning_rate and momentum are for the opimizer learning_rate = 0.01 momentum = 0.5 log_interval = 10 random_seed = 1 torch.backends.cudnn.enabled = False torch.manual_seed(random_seed) <torch._C.Generator at 0x2048010c690>
Now we are going to load the MNIST dataset using TorchVision. We are using the batch_size of 64 for training and size 1000 for testing on this dataset. For normalization, we’ll use the mean value of 0.1307 and standard deviation of 0.3081 of the MNIST dataset.
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/files/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])
),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/files/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])
),
batch_size=batch_size_test, shuffle=True)
Output
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz Processing... Done!
Use test_loader to load test data
examples = enumerate(test_loader) batch_idx, (example_data, example_targets) = next(examples) example_data.shape
Output
torch.Size([1000, 1, 28, 28])
So from the output we can see we have one test data batch is a tensor of shape: [1000, 1, 28, 28] means- 1000 examples of 28*28 pixels in grayscale.
Lets plot some of the dataset using matplotlib.
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(5):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Ground Truth: {}".format(example_targets[i]))
plt.xticks([])
plt.yticks([])
print(fig)
Output

Building the Network
Now we are going to build our network using 2-D convolutional layers followed by two fully-connected layers. We are going to create a new class for the network we wish to build but before that let’s import some modules.
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x)
Initialize the network and the optimizer:
network = Net() optimizer = optim.SGD(network.parameters(), lr = learning_rate,momentum = momentum)
Training the Model
Let's build our training model. So first check our network is in network mode and then interate overall training data once per epoch. Dataloader will load the individual batches. We set the gradients to zero using optimizer.zero_grad()
train_losses = [] train_counter = [] test_losses = [] test_counter = [i*len(train_loader.dataset) for i in range(n_epochs + 1)]
To create a nice training curve, we create two lists for saving training and testing losses. On the x-axis we want to display the number of training examples.
The backward() call we now collect a new set of gradients which we propagate back into each of the network’s parameters using optimizer.step().
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
train_losses.append(loss.item())
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
torch.save(network.state_dict(), '/results/model.pth')
torch.save(optimizer.state_dict(), '/results/optimizer.pth')
Neutral network modules, as well as optimizers, have the ability to save and load their internal state using .state_dict().
Now for our test loop, we sum up the test loss and keep track of correctly classified digits to compute the accuracy of the network.
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
To run the training, we add a test() call before we loop over n_epochs to evaluate our model with randomly initialized parameters.
test() for epoch in range(1, n_epochs + 1): train(epoch) test()
Output
Test set: Avg. loss: 2.3048, Accuracy: 1063/10000 (10%) Train Epoch: 1 [0/60000 (0%)]Loss: 2.294911 Train Epoch: 1 [640/60000 (1%)]Loss: 2.314225 Train Epoch: 1 [1280/60000 (2%)]Loss: 2.290719 Train Epoch: 1 [1920/60000 (3%)]Loss: 2.294191 Train Epoch: 1 [2560/60000 (4%)]Loss: 2.246799 Train Epoch: 1 [3200/60000 (5%)]Loss: 2.292224 Train Epoch: 1 [3840/60000 (6%)]Loss: 2.216632 Train Epoch: 1 [4480/60000 (7%)]Loss: 2.259646 Train Epoch: 1 [5120/60000 (9%)]Loss: 2.244781 Train Epoch: 1 [5760/60000 (10%)]Loss: 2.245569 Train Epoch: 1 [6400/60000 (11%)]Loss: 2.203358 Train Epoch: 1 [7040/60000 (12%)]Loss: 2.192290 Train Epoch: 1 [7680/60000 (13%)]Loss: 2.040502 Train Epoch: 1 [8320/60000 (14%)]Loss: 2.102528 Train Epoch: 1 [8960/60000 (15%)]Loss: 1.944297 Train Epoch: 1 [9600/60000 (16%)]Loss: 1.886444 Train Epoch: 1 [10240/60000 (17%)]Loss: 1.801920 Train Epoch: 1 [10880/60000 (18%)]Loss: 1.421267 Train Epoch: 1 [11520/60000 (19%)]Loss: 1.491448 Train Epoch: 1 [12160/60000 (20%)]Loss: 1.600088 Train Epoch: 1 [12800/60000 (21%)]Loss: 1.218677 Train Epoch: 1 [13440/60000 (22%)]Loss: 1.060651 Train Epoch: 1 [14080/60000 (23%)]Loss: 1.161512 Train Epoch: 1 [14720/60000 (25%)]Loss: 1.351181 Train Epoch: 1 [15360/60000 (26%)]Loss: 1.012257 Train Epoch: 1 [16000/60000 (27%)]Loss: 1.018847 Train Epoch: 1 [16640/60000 (28%)]Loss: 0.944324 Train Epoch: 1 [17280/60000 (29%)]Loss: 0.929246 Train Epoch: 1 [17920/60000 (30%)]Loss: 0.903336 Train Epoch: 1 [18560/60000 (31%)]Loss: 1.243159 Train Epoch: 1 [19200/60000 (32%)]Loss: 0.696106 Train Epoch: 1 [19840/60000 (33%)]Loss: 0.902251 Train Epoch: 1 [20480/60000 (34%)]Loss: 0.986816 Train Epoch: 1 [21120/60000 (35%)]Loss: 1.203934 Train Epoch: 1 [21760/60000 (36%)]Loss: 0.682855 Train Epoch: 1 [22400/60000 (37%)]Loss: 0.653592 Train Epoch: 1 [23040/60000 (38%)]Loss: 0.932158 Train Epoch: 1 [23680/60000 (39%)]Loss: 1.110188 Train Epoch: 1 [24320/60000 (41%)]Loss: 0.817414 Train Epoch: 1 [24960/60000 (42%)]Loss: 0.584215 Train Epoch: 1 [25600/60000 (43%)]Loss: 0.724121 Train Epoch: 1 [26240/60000 (44%)]Loss: 0.707071 Train Epoch: 1 [26880/60000 (45%)]Loss: 0.574117 Train Epoch: 1 [27520/60000 (46%)]Loss: 0.652862 Train Epoch: 1 [28160/60000 (47%)]Loss: 0.654354 Train Epoch: 1 [28800/60000 (48%)]Loss: 0.811647 Train Epoch: 1 [29440/60000 (49%)]Loss: 0.536885 Train Epoch: 1 [30080/60000 (50%)]Loss: 0.849961 Train Epoch: 1 [30720/60000 (51%)]Loss: 0.844555 Train Epoch: 1 [31360/60000 (52%)]Loss: 0.687859 Train Epoch: 1 [32000/60000 (53%)]Loss: 0.766818 Train Epoch: 1 [32640/60000 (54%)]Loss: 0.597061 Train Epoch: 1 [33280/60000 (55%)]Loss: 0.691049 Train Epoch: 1 [33920/60000 (57%)]Loss: 0.573049 Train Epoch: 1 [34560/60000 (58%)]Loss: 0.405698 Train Epoch: 1 [35200/60000 (59%)]Loss: 0.480660 Train Epoch: 1 [35840/60000 (60%)]Loss: 0.582871 Train Epoch: 1 [36480/60000 (61%)]Loss: 0.496494 …… …… ……. Train Epoch: 3 [49920/60000 (83%)]Loss: 0.253500 Train Epoch: 3 [50560/60000 (84%)]Loss: 0.364354 Train Epoch: 3 [51200/60000 (85%)]Loss: 0.333843 Train Epoch: 3 [51840/60000 (86%)]Loss: 0.096922 Train Epoch: 3 [52480/60000 (87%)]Loss: 0.282102 Train Epoch: 3 [53120/60000 (88%)]Loss: 0.236428 Train Epoch: 3 [53760/60000 (90%)]Loss: 0.610584 Train Epoch: 3 [54400/60000 (91%)]Loss: 0.198840 Train Epoch: 3 [55040/60000 (92%)]Loss: 0.344225 Train Epoch: 3 [55680/60000 (93%)]Loss: 0.158644 Train Epoch: 3 [56320/60000 (94%)]Loss: 0.216912 Train Epoch: 3 [56960/60000 (95%)]Loss: 0.309554 Train Epoch: 3 [57600/60000 (96%)]Loss: 0.243239 Train Epoch: 3 [58240/60000 (97%)]Loss: 0.176541 Train Epoch: 3 [58880/60000 (98%)]Loss: 0.456749 Train Epoch: 3 [59520/60000 (99%)]Loss: 0.318569 Test set: Avg. loss: 0.0912, Accuracy: 9716/10000 (97%)
Evaluating the Model’s Performance
So with only 3 epochs of training we managed to achieve 97% accuracy on the test set. With randomly initialized parameters, we started with 10% accuracy on the test set initially, before starting the training.
Lets plot our training curve:
fig = plt.figure()
plt.plot(train_counter, train_losses, color='blue')
plt.scatter(test_counter, test_losses, color='red')
plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
plt.xlabel('number of training examples seen')
plt.ylabel('negative log likelihood loss')
fig
Output
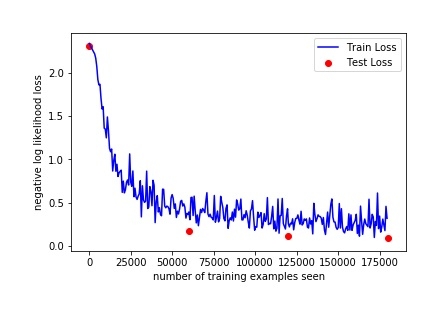
By checking above output, we can increase the number of epochs to see some more results,As the accuracy is increased by checking the 3 epoches.
But before that, run some few more examples and compare the model’s output:
with torch.no_grad():
output = network(example_data)
fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Prediction: {}".format(
output.data.max(1, keepdim=True)[1][i].item()))
plt.xticks([])
plt.yticks([])
fig

As we can see our models predictions, it looks similar to be on point for those examples.

