Temperature Coefficient of Resistance – Definition, Formula and Examples

The electrical and electronic components such as resistors, capacitors, inductors, wires, cables, insulators, etc. are made up of different types of material. We generally refer all these materials as engineering materials. Based on electrical resistivity, the engineering materials are categorized into three categories namely – conductors, semiconductors, and insulators.

Since every material present in the nature possess a finite amount of electrical resistance. Also, this resistance can change with the variation in the temperature. The following points briefly explain the variation in resistance of the different types of materials with the change in temperature −

• The resistance of conductors increases with the rise in its temperature.
• The resistance of semiconductors decrease with the increase in temperature.
• The resistance of insulating materials also decrease with the increase in temperature.

The change in the resistance of a material with the change in its temperature is expressed in terms of the temperature coefficient of resistance.

In this article, we will discuss the temperature coefficient of resistance, its definition, derivation, formula, and examples. So let’s begin with the definition of temperature coefficient of resistance.

What is the Temperature Coefficient of Resistance?

The measure of change in the electrical resistance of a material with per unit change in the temperature is referred to as the temperature coefficient of resistance. It is denoted by the Greek letter alpha (α).

Experimentally, it has been found that in the normal range of temperatures −

• The change in resistance is directly proportional to the initial resistance, i.e.,

$$\mathrm{\Delta R\propto R_{0}}$$

Where,

$$\mathrm{\Delta R=R_{t}- R_{0}}$$

And, 𝑅₀ is the initial resistance of the material, and Rt is the resistance of the material at any t °C.

• The change in resistance is directly proportional to the rise in temperature, i.e.,

$$\mathrm{\Delta R\propto t-0=t}$$

• The change in resistance depends upon the nature the material.

Combining the first two points, we have,

$$\mathrm{\Delta R\propto R_{0}t}$$

$$\mathrm{\Rightarrow \Delta R=\alpha _{0} R_{0}t\: \cdot \cdot \cdot \left ( 1 \right )}$$

Also,

$$\mathrm{R_{t}-R_{0}=\alpha _{0}R_{0}t\: \cdot \cdot \cdot \left ( 2 \right )}$$

Or,

$$\mathrm{R_{t}=R_{0}\left ( 1+\alpha _{0}t \right )\: \cdot \cdot \cdot \left ( 3 \right )}$$

Where, α₀ is a constant of proportionality, and is called the temperature coefficient of resistance of material at 0 °C.

On rearranging the equation (2), we get,

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}t}\: \cdot \cdot \cdot \left ( 4 \right )}$$

Hence, the temperature coefficient of resistance of a material is the change in resistance per ohm original resistance per °C change in temperature. The unit of temperature coefficient is per degree Celsius (/°C).

Since, the value of temperature coefficient of resistance at 0 °C (α₀) is different for different materials. Thus, the change in resistance of different materials is different for the same change in the temperature. That is why, conductors, semiconductors, and insulators shows different variations in resistance with the same change in the temperature.

In case of conductors, the value of ΔR is positive, i.e. the resistance of conductors increase with rise in temperature. Thus, the temperature coefficient of resistance for conductors is positive. But, in the resistance of semiconductors and insulators decrease with the increase in temperature. Thus, the temperature coefficient of resistance for semiconductors and insulators is negative.

Graphical Determination of Temperature Coefficient of Resistance

We can also determine the value of temperature coefficient of resistance graphically with the help of temperature-resistance graph of a substance. Consider a typical temperatureresistance graph for a conductor as shown in Figure-1.

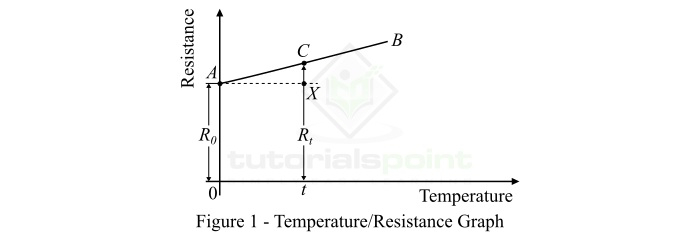
For conductors, the plot of the temperature-resistance graph is a straight line. Here, the resistance of the conductor is 𝑅₀ at 0 °C as represented by OA. The resistance of conductor at temperature t °C is R_t.

Thus, by the definition of the temperature coefficient of resistance, we have,

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}\times t}}$$

From the temperature-resistance graph,

$$\mathrm{R_{t}-R_{0}=XC}$$

And,

$$\mathrm{Rise\: in\: temp.=t=AX}$$

Therefore, the temperature coefficient of resistance of the conductor at 0 °C is,

$$\mathrm{\alpha _{0}=\frac{XC}{R_{0}\times AX}}$$

But, the slope of the temperature-resistance graph is,

$$\mathrm{Slope\: of\: graph=\frac{XC}{AX}}$$

Therefore,

$$\mathrm{\alpha _{0}=\frac{Slope\: of\: temp.\: resistance graph}{Initial\: reisstance}\: \cdot \cdot \cdot \left ( 5 \right )}$$

Hence, the temperature coefficient of resistance of a substance at 0 °C is the slope of the temperature-resistance graph divided by the initial resistance of the substance (or the resistance at 0 °C, i.e., 𝑅₀).

Temperature Coefficient of Resistance at any Temperature

For a material, if the temperature coefficient of resistance at 0 °C (i.e., 𝛼₀) is known. Then, we can determine the value of temperature coefficient of resistance of the material at any temperature by using the following expression,

$$\mathrm{\alpha _{t}=\frac{\alpha _{0}}{1+\alpha _{0}t}\: \cdot \cdot \cdot \left ( 6 \right )}$$

Where, _𝛼0 is the temperature coefficient of resistance at t °C.

Note − The temperature coefficient of resistance helps us to determine the value of resistance of the material at different temperatures. Let 𝑅₁ and 𝑅₂ are the resistances of a material at 𝑡₁°C and 𝑡₂°C respectively. If α₁ is the temperature coefficient of resistance at 𝑡₁°C. Then, the resistance of the material R₂ is given by,

$$\mathrm{R_{2}=R_{1}\left [ 1+\alpha _{1}\left ( t_{2}-t_{1} \right ) \right ]\: \cdot \cdot \cdot \left ( 7 \right )}$$

Temperature Coefficient of Resistance of Some Materials

The following table gives the value of the temperature coefficient of resistance of some materials at standard temperature (20 °C), which are used in electrical, electronics and other engineering fields −

S. No.	Material	Temperature Coefficient of Resistance at 20 °C (in /°C)
6.	Iron (Fe)	0.00651
12.	Nickel (Ni)	0.00641
5.	Tungsten (W)	0.0045
4.	Aluminium (Al)	0.00429
13.	Tin (Sn)	0.0042
7.	Platinum (Pt)	0.003927
2.	Copper (Cu)	0.00386
1.	Silver (Ag)	0.0038
3.	Gold (Au)	0.0034
8.	Mercury (Hg)	0.0009
14.	Nichrome (Ni-Cr-Fe)	0.0004
16.	Constantan (Cu-Ni)	0.00003
15.	Manganin (Cu-Mn-Ni)	0.000002
9.	Carbon (C)	-0.0005
10.	Germanium (Ge)	-0.05
11.	Silicon (Si)	-0.07

Numerical Example (1)

The field winding of an electric motor has a resistance of 15 Ω at 0 °C and 18 Ω at 30 °C. Find the temperature coefficient of resistance of the field winding at 0 °C.

Solution

Given data,

• 𝑅₀ = 15 Ω
• 𝑅₃₀ = 18 Ω

Since, the temperature coefficient of resistance at 0 °C is given by,

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}\times t}}$$

In this case, t = 30 °C, thus,

$$\mathrm{\alpha _{0}=\frac{R_{30}-R_{0}}{R_{0}\times 30}=\frac{18-15}{15\times 30}}$$

$$\mathrm{\therefore \alpha _{0}=0.00667\: _{}^{\circ }\textrm{C}^{-1}}$$

Numerical Example (2)

The shunt winding of a DC generator is made up of copper wire and has a temperature coefficient of resistance 0.00426 /°C at 0 °C. Determine the temperature coefficient of resistance of the winding at 27 °C.

Solution

Given data,

• 𝛼₀ = 0.00426

The temperature coefficient of resistance at 27 °C is given by,

$$\mathrm{ \alpha _{27}=\frac{\alpha _{0}}{1+27\alpha _{0}}}$$

$$\mathrm{\Rightarrow \alpha _{27}=\frac{0.00426}{1+\left ( 27\times 0.00426 \right )}}$$

$$\mathrm{\therefore \alpha _{27}=0.00382\, _{}^{\circ }\textrm{C}^{-1}}$$

Numerical Example (3)

The stator winding of a motor has a resistance of 90 Ω at 17 °C. Find its resistance at 50 °C, if its temperature coefficient of resistance is 0.003 at 17 °C.

Solution

Given data,

• 𝑅₁₇ = 90 Ω
• 𝛼₁₇ = 0.003

Then, the resistance of the winding at 50 °C is given by,

$$\mathrm{R_{50}=R_{17}\left [ 1+\alpha _{17}\left ( 50-17 \right ) \right ]}$$

$$\mathrm{\Rightarrow R_{50}=90\times \left [ 1+0.003\times 33 \right ]}$$

$$\mathrm{\therefore R_{50}=98.91\, \Omega }$$

Conclusion

We will conclude this article with the following points −

• The electrical resistance of materials changes with the variation in temperature.

• The change in resistance of materials is described by a factor known as temperature coefficient of resistance of the material.

• The temperature coefficient of resistance helps us in selecting a material suitable for a particular application.

• The temperature coefficient of resistance can also be used to determine the resistance of a material at a particular temperature.

• For metals, the temperature coefficient of resistance is positive, which indicates that the resistance of metals increases with the increase in temperature and vice-versa.

For semiconductors and insulators, the temperature coefficient of resistance is negative, which indicates that the resistance of semiconductors and insulators decreases with the increase in temperature and vice-versa.