Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Mutual Inductance: Definition & Formula
When the two coils are arranged in such a way that a change of current in one coil causes an emf to be induced in the other, the coils are said to have mutual inductance. The mutual inductance is denoted letter M and measured in Henry.
Consider two coils, coil 1 and coil 2 placed adjacent to each other. When a current I1 flows in the coil 1, a magnetic flux (Φ1) is produced in it and some part of the Φ1 links with the coil 2 and is known as mutual flux (Φm).
Now, if the current in the coil 1 changes, the mutual flux also changes, therefore an EMF is induced in the coil 2. This induced emf in the coil 2 is known as mutually induced emf (𝑒𝑚). This mutually induced emf is responsible for the mutual inductance between the coils. The effect of mutual inductance is to either increase or decrease the total inductance of the two coils depending upon the arrangement of the coils.
Mutual Inductance Formula
The mutual inductance (M) between two coils can be determined by using any one of the following three methods depending upon the known quantities −
Method 1
If the magnitude of mutually induced emf (𝑒𝑚) in one coil and the rate of change of current in the other coil are known, then mutual inductance (M) is given by,
$$\mathrm{e_{m}=M\frac{dl_{1}}{dt}}$$
$$\mathrm{\Rightarrow\:M=\frac{e_{m}}{(dl_{1}/dt)}\:\:\:...(1)}$$
Method 2
Consider two magnetically coupled coils, coil 1 and coil 2, having N1 and N2 turns respectively. If a current I1 flowing in the coil 1, a mutual flux (Φm) is produced that links the coil 2. Therefore,
$$\mathrm{{m}=M\frac{dl_{1}}{dt}=\frac{d}{dt}(Ml_{1})}$$
Also, the mutually induced emf is given by,
$$\mathrm{e_{m}=N_{2}\frac{d\phi_{m}}{dt}=\frac{d}{dt}(N_{2}\phi_{m})}$$
Thus, by equating these two equations, we get,
$$\mathrm{Ml_{1}=N_{2}\phi_{m}}$$
$$\mathrm{\Rightarrow\:M=\frac{N_{2}\phi_{m}}{l_{1}}\:\:\:...(2)}$$
Method 3
If the physical dimensions of the magnetic circuit are known, then the mutual inductance of it can be determined as follows −
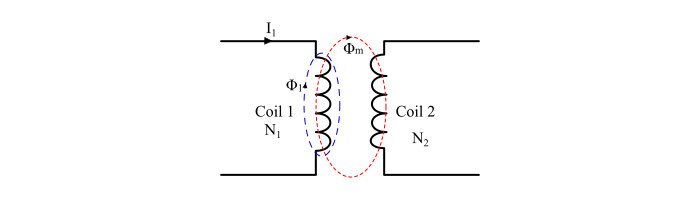
Let, the ‘l’ and ‘a’ be the length and cross-sectional areal of the magnetic circuit. The N1 and N2 are number of turns in the coil 1 and coil 2 respectively.
Mutual flux,
$$\mathrm{\phi_{m}=\frac{MMF}{Reluctance(s)}=\frac{N_{1}l_{1}}{(1/\mu_{0}\mu_{r}a)}}$$
Where,
μ𝑟 = relative permeability of material of magnetic circuit,
μ0 = absolute permeability of vacuum or air.
$$\mathrm{\Rightarrow\:\frac{\phi_{m}}{l_{1}}=\frac{N_{1}}{(1/\mu_{0}\mu_{r}a)}}$$
$$\mathrm{(\because\:M=\frac{N_{2}\phi_{m}}{l_{1}})}$$
$$\mathrm{M=N_{2}(\frac{N_{1}}{1/\mu_{0}\mu_{r}a})}$$
$$\mathrm{\Rightarrow\:M=(\frac{N_{1}N_{2}}{1/\mu_{0}\mu_{r}a})=\frac{{N_{1}N_{2}}}{Reluctance(S)}\:\:\:\:...(3)}$$
Method 4
If two coils have self-inductances L1 and L2, then the mutual inductance can also be given as,
$$\mathrm{M=k\sqrt{L_{1}L_{2}}\:\:\:...(4)}$$
Where, k is the coefficient of coupling.
1K+ Views
