Conductance and Conductivity – Definition, Unit, Formula and Examples

In this article, we shall discuss electrical conductance and conductivity, its definition, formula, unit of measurement, and the solved numerical examples.

What is Electrical Conductance?

The measure of how easily the electric charge (or electrons or electric current) can flow through a material is called the conductance or electrical conductance of that material.

Therefore, electrical conductance defines the capability of a substance to conduct electricity. In order to understand the concept of electrical conductance, we have to recall the electrical resistance of materials.

Electrical resistance is defined as the measure of difficulty that a material offers in the flow of electric current or electric charge. The resistance is mainly the result of collisions of electric charges with ions of the atom within the material.

Thus, a material in which the number of collisions of electric charges with the ions of atoms is less, the conductance of the material will be more and vice-versa, and therefore, this material conducts the electric current more easily. Hence, this discussion shows that electrical conductance is the property of a material opposite to electrical resistance.

Formula and Unit of Conductance

In electrical and electronic circuits, electrical conductance is defined as the reciprocal of resistance of a conductor. It is represented by the symbol ‘G’.

$$\mathrm{\therefore Conductance,\, G\, =\, \frac{1}{Resistance\left ( R \right )}\: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

According to Ohm’s law, the resistance of a conductor is given by,

$$\mathrm{Resistance,\, R\, =\, \frac{V}{I}}$$

Where, V is the voltage across and I is the current through the conductor.

$$\mathrm{\therefore G\, =\, \frac{I}{V}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$

Also, the resistance of a conductor can be expressed in terms of the physical dimensions of the conductor as,

$$\mathrm{R\, =\, \frac{\rho l}{a}}$$

Therefore, the conductance of a conductor in terms of its physical dimensions will be,

$$\mathrm{G\, =\, \frac{a}{\rho l}\, =\, \sigma \frac{a}{ l}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

Where, σ is called conductivity or specific conductance of the conductor material.

$$\mathrm{\therefore \sigma \, =\, \frac{1}{\rho}}$$

Unit of Conductance

As the conductance of a conductor is given by,

$$\mathrm{G=\frac{1}{R}=\frac{I}{V}=\frac{\sigma a}{l}}$$

$$\mathrm{\therefore Unit\: of\: G=\frac{1}{Ohm\, \left ( \Omega \right )}=\frac{Ampere}{Volt}=Mho}$$

Thus, the unit of conductance is Mho (Ω^-1). But, in practice, we commonly use Siemen (S) as the unit of conductance. Where,

$$\mathrm{1\: Mho (\Omega ) = 1\: \: Siemen}$$

Factors Affecting the Conductance

From equation (3), we have,

$$\mathrm{G=\frac{\sigma a}{l}}$$

Thus, the conductance of a conductor is −

• Directly proportional to the cross-sectional area of the conductor.

• Inversely proportional to the length of the conductor.

• Dependent upon the nature of the material (σ).

• Varied with the temperature.

What is Conductivity?

The ability of a substance to provide ease in the flow of electric current or charge through it is called conductivity. It is denoted by the Greek letter sigma (σ).

Conductivity is one of the most important properties of substances that is used to select suitable material for making electrical conductors and insulators. Where, if a material has high conductivity, then it is best suited for making conducting wires, and if a material has low conductivity, then it is suitable for making insulators.

Basically, electrical conductivity explains the behavior of material for current flow on the application of an electric field.

Mathematically, the conductivity of a material is expressed as the reciprocal of its resistivity, i.e.,

$$\mathrm{Conductivity,\sigma =\frac{1}{Resistivity\left ( \rho \right )}\cdot \cdot \cdot \left ( 4 \right )}$$

The conductivity is also known as specific conductance. The conductivity is measured in Siemens per meter (S/m) or mho per meter (Ω^-1m^-1).

Conductance of Series Circuits

Consider a series resistive circuit as shown in Figure1. The circuit consists of three resistors connected in series.

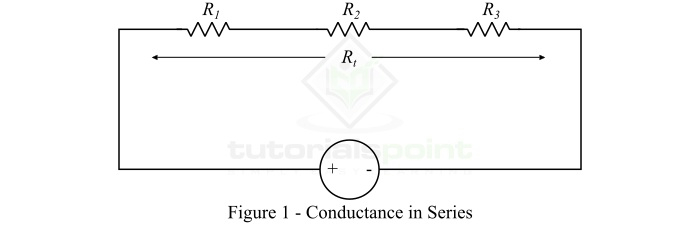
From the circuit, we have,

$$\mathrm{R_{t}=R_{1}\, +\,R_{2}\, +\,R_{3} }$$

$$\mathrm{ \because Conductance, G=\frac{1}{R}}$$

Therefore,

$$\mathrm{ \frac{1}{G_{t}}=\frac{1}{R_{1}}\, +\,\frac{1}{R_{2}}\, +\,\frac{1}{R_{3}}\, \, \cdot \cdot \cdot \left ( 5 \right ) }$$

Also,

$$\mathrm{G_{t}=\frac{1}{R_{t}}=\frac{1}{R_{1}\, +\,R_{2}\, +\,R_{3}} \, \, \cdot \cdot \cdot \left ( 6 \right )}$$

Hence, when a number of resistors are connected in series, then the reciprocal of total conductance is equal to the sum of the reciprocal of conductance of the individual resistors.

Conductance of Parallel Circuits

Consider a parallel circuit as shown in Figure2. It consists of three resistors connected in parallel.

From the circuit, we can write,

$$\mathrm{ \frac{1}{R_{t}}=\frac{1}{R_{1}}\, +\,\frac{1}{R_{2}}\, +\,\frac{1}{R_{3}} }$$

From the definition of conductance, we have,

$$\mathrm{ G=\frac{1}{R}}$$

Therefore,

$$\mathrm{ G_{t}=G_{1}\, +\,G_{2}\, +\,G_{3}\: \: \cdot \cdot \cdot \left ( 7 \right ) }$$

Hence, when a number of resistors are connected in parallel, then the total conductance of the circuit is equal to the sum of the conductance of the individual resistors.

Conductance vs. Conductivity

The conductance of a conductor is the measure of how easily the material of the conductor allows the flow of current through it. Whereas, conductivity is the property of a material by virtue of which the material offers ease in the flow of current.

Numerical Example

Calculate the conductance of a wire of 915 m having a uniform cross-section of 0.88 cm². The wire is made up of copper having a conductivity of 5.9 × 10⁵ S/m.

Solution

Given data,

$$\mathrm{length, l = 915 m }$$

$$\mathrm{Area\: of\: cross\: section, a = 0.88\: \: cm^{2} = 0.88 \times 10^{-4}\: m^{2} }$$

$$\mathrm{Conductivity, \sigma = 5.9\times 10^{5}\: Sm^{-1} }$$

Therefore, the conductance of the wire will be,

$$\mathrm{G=\frac{\sigma a}{l}=\frac{\left ( 5.9\times 10^{5} \right )\times \left ( 0.88\times 10^{-4} \right )}{\left ( 915 \right )}}$$

$$\mathrm{\therefore G=0.0867\: S}$$