What is Permeance – Definition, Formula, Units, Coefficient and Example

In this article, we shall learn about Permeance in magnetic circuits, its definition, formula, unit of measurement, and coefficient.

What is Permeance?

The measure of the ease with which the magnetic flux can flow through a magnetic material is called Permeance. It is denoted by the symbol P and given by the following expression,

$$\mathrm{Permeance,\, P=\frac{1}{Reluctance}\: \: \cdot \cdot \cdot \left ( 1 \right )}$$

Hence, the Permeance may also be defined as the reciprocal of magnetic reluctance. Where, magnetic reluctance is the measure of opposition that a magnetic material or a magnetic circuit offers in the path of magnetic flux.

It is experimentally observed that the Permeance of a magnetic material is directly proportional to the magnetic flux passing through it, and inversely proportional to the MMF (magnetomotive force). Therefore, we have,

$$\mathrm{P=\frac{\phi }{NI}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$

This expression shows that if the Permeance of a magnetic circuit is low, then it requires a large MMF to establish a certain amount of magnetic flux in it.

The Permeance of a magnetic circuit can also be expressed in terms of the physical parameters of the circuit as,

$$\mathrm{P=\frac{\mu A }{l}=\frac{\mu_{0}\mu_{r} A }{l}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

Where,

• A is the area of cross-section of the circuit,
• l is the mean length of the magnetic circuit,
• $\mathrm{\mu_{0}}$ is the permeability of free space, which is equal to 4Ï€ × 10^-7 H/m, and
• $\mathrm{\mu_{r}}$ is the relative permeability of the magnetic material

Thus, from this equation, it can be observed that the Permeance of a magnetic circuit increases with the increased cross-sectional area and decreases with the increase in length of the magnetic circuit.

What is the Unit of Permeance?

As the Permeance is given by the ratio of magnetic flux in the magnetic circuit to the MMF required to establish this flux, i.e.,

$$\mathrm{P=\frac{Magneti\: Flux }{MMF}=\frac{Weber }{Ampere \: Turn}}$$

Therefore, the Permeance is measured in weber per ampere turn (Wb/AT).

Also,

$$\mathrm{1\: Wb/AT = 1\: Henry (H)}$$

What is Permeance Coefficient?

The ratio of magnetic flux density to the magnetic field intensity at the operating point of the B-H curve is called the Permeance coefficient. It is usually represented by the symbol P_C.

$$\mathrm{Permeance\: coefficient,P_{c} = \frac{B_{0}}{H_{0}}\: \: \:\cdot \cdot \cdot \left ( 4 \right )}$$

Where, B₀ is the magnetic flux density, and H₀ is the magnetic field intensity at the operating point of the B-H curve.

The Permeance coefficient is one of the important parameters in the magnetic circuit design as it is used to determine the operating point of the magnetic circuit on the B-H curve.

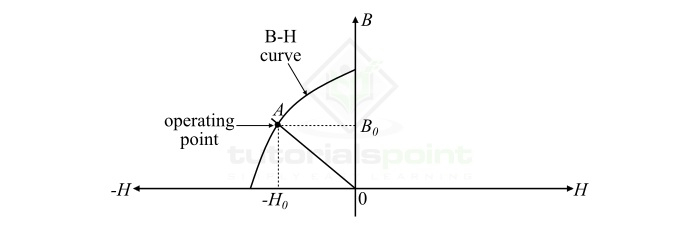
A typical B-H curve is shown in the figure. Here, the straight line OA passing through the origin cuts the B-H curve at point A, which is called the operating point of the magnetic circuit. The line OA is known as the Permeance line, and the slope of the Permeance line OA (i.e. B₀ / H₀) is known as the Permeance coefficient.

Numerical Example

A magnetic circuit is built up of an iron core of 9 cm² cross-sectional area. The mean length of the magnetic circuit is 20 cm, and the relative permeability of the core material is 1000. Find the Permeance of the magnetic circuit.

Solution

Given data,

$$\mathrm{Area\: of\: cross\: section, A = 9\, cm^2 = 9 \times 10^{-4}\, m}$$

$$\mathrm{Mean\: length\: of\: the\: circuit, l = 20\, cm = 20 \times 10^{-2} m}$$

$$\mathrm{Relative\: permeability, \mu _{r} = 1000}$$

Then, the Permeance of the magnetic circuit is given by,

$$\mathrm{P=\frac{\mu _{0}\mu _{r}A}{l}}$$

$$\mathrm{\Rightarrow P=\frac{(4\pi \times 10^{-7}) \times (1000) \times (9 \times 10^{-4})}{(20 \times 10^{-2})}=5.652 \times 10^{-6} \: Wb/AT}$$