Swinburne’s Test of DC Machine – Testing of DC Machines

Swinburne’s test is an indirect method of testing DC machines, named after Sir James Swinburne. In this method, the losses are determined separately and the efficiency at desired load is predetermined. The Swinburne’s test is the simplest method of testing of shunt and compound DC machines which have constant field flux.

The connection diagram is shown in the figure and the machine is run as a motor at rated voltage and speed.

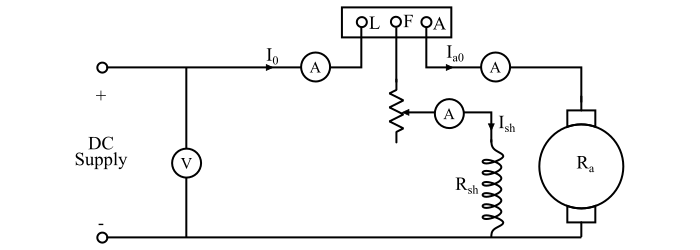
Let,

$$\mathrm{𝑉 = Supply\:voltage}$$

$$\mathrm{𝐼_{0} = No \:load \:line\: current}$$

$$\mathrm{𝐼_{sh} = Shunt\: field \:current}$$

$$\mathrm{\therefore \:No \:load\: armature \:current,\:I_{𝑎0} = I_{0} − I_{sh}}$$

And

$$\mathrm{No load input power = 𝑉𝐼_{0}}$$

This no-load input power of the machine supplies the following −

• Core loss
• No-load armature cu loss
• Friction and windage losses

At no-load the useful mechanical output of the machine is zero, thus the no-load input power is only used to supply the losses in the machine. Hence,

$$\mathrm{Armature\:cu − loss\:at\:no − load = (𝐼_{𝑎0})^2𝑅_{𝑎}}$$

Where, R_a is the resistance of armature winding.

Therefore, the constant power losses in the machine will be,

$$\mathrm{𝑃_{𝐶} = No\:load \:input\: power − No \:load \:armature \:cu\: loss}$$

$$\mathrm{⇒ 𝑃_{𝐶} = 𝑉𝐼_{0} − (𝐼_{𝑎0})^2𝑅_{𝑎}}$$

Now, after knowing the constant losses of the machine, its efficiency at any other load can be determined as follows −

Consider "I" is the load current at which the efficiency of the machine is to be calculated.

Efficiency when Running as Motor

Here,

$$\mathrm{Armature\:current,\:I_{a} = I − I_{sh}}$$

$$\mathrm{Motor\:input\:power = VI}$$

$$\mathrm{Armature\:Cu\:loss = I_{a}^{2}R_{𝑎} = (I − I_{sh})^2𝑅_{𝑎}}$$

$$\mathrm{\therefore\: Total \:losses\: in\: the\: machine = (I − 𝐼_{sh})^2𝑅_{𝑎} + 𝑃_{𝐶}}$$

Where, P_C is the constant losses which is determined above.

Therefore,

$$\mathrm{Efficiency\:of\:Motor,\: \eta_{𝑚} =\frac{Output}{Input} =\frac{Input − Losses}{Input}}$$

$$\mathrm{⇒ \eta_{𝑚} =\frac{𝑉𝐼 − (I − 𝐼_{sh})^2𝑅_{𝑎} − 𝑃_{𝐶}}{𝑉𝐼}}$$

Efficiency when Running as Generator

Here,

$$\mathrm{Armature\:current,\:I_{a} = I + I_{sh}}$$

$$\mathrm{Generator\:output \:power = VI}$$

$$\mathrm{Armature\:Cu\:loss = I_{a}^{2}R_{𝑎} = (I + I_{sh})^2𝑅_{𝑎}}$$

$$\mathrm{\therefore\: Total \:losses\: in\: the\: machine = (I + 𝐼_{sh})^2𝑅_{𝑎} + 𝑃_{𝐶}}$$

$$\mathrm{Efficiency\: of \:Generator,\: \eta_{𝑔} =\frac{Output}{Output + Losses} =\frac{𝑉𝐼}{𝑉𝐼 + (I + 𝐼_{sh})^2𝑅_{𝑎} + 𝑃_{𝐶}}}$$

Advantages of Swinburne’s Test

Following are the advantages of Swinburne’s test −

• The power required for the testing of large machines is very small, therefore it is an economical and convenient method of testing DC machines.
• As the constant losses are known, thus the efficiency can be pre-determined at any load.

Disadvantages of Swinburne’s Test

The main disadvantages of the Swinburne’s test are −

• The change in iron losses is not considered from no-load to full load. At full load, due to the armature reaction, the flux is distorted which increases the iron losses.
• Since the Swinburne’s test is performed on no-load, thus it does not indicate whether the commutation on full load is satisfactory and whether the temperature rise would be within specified limits.

Limitations of the Swinburne’s Test

The Swinburne’s test has the following limitation −

• The Swinburne’s test is only applicable only to those DC machines in which the flux is practically constant, which are shunt machines and level compound generators.
• The series DC machines cannot be test by Swinburne’s test since they cannot be run on no-load and their flux and speed very greatly.