Satellite Communication - Orbital Mechanics

We know that the path of satellite revolving around the earth is known as orbit. This path can be represented with mathematical notations. Orbital mechanics is the study of the motion of the satellites that are present in orbits. So, we can easily understand the space operations with the knowledge of orbital motion.

Orbital Elements

Orbital elements are the parameters, which are helpful for describing the orbital motion of satellites. Following are the orbital elements.

Semi major axis
Eccentricity
Mean anomaly
Argument of perigee
Inclination
Right ascension of ascending node

The above six orbital elements define the orbit of earth satellites. Therefore, it is easy to discriminate one satellite from other satellites based on the values of orbital elements.

Semi major axis

The length of Semi-major axis (a) defines the size of satellite’s orbit. It is half of the major axis. This runs from the center through a focus to the edge of the ellipse. So, it is the radius of an orbit at the orbit's two most distant points.

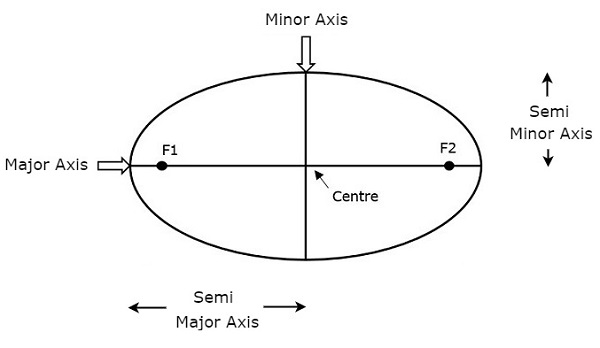
Both semi major axis and semi minor axis are represented in above figure. Length of semi major axis (a) not only determines the size of satellite’s orbit, but also the time period of revolution.

If circular orbit is considered as a special case, then the length of semi-major axis will be equal to radius of that circular orbit.

Eccentricity

The value of Eccentricity (e) fixes the shape of satellite’s orbit. This parameter indicates the deviation of the orbit’s shape from a perfect circle.

If the lengths of semi major axis and semi minor axis of an elliptical orbit are a & b, then the mathematical expression for eccentricity (e) will be

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

The value of eccentricity of a circular orbit is zero, since both a & b are equal. Whereas, the value of eccentricity of an elliptical orbit lies between zero and one.

The following figure shows the various satellite orbits for different eccentricity (e) values

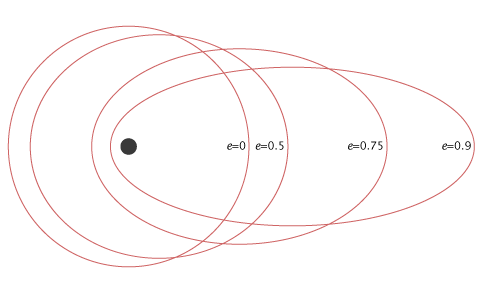
In above figure, the satellite orbit corresponding to eccentricity (e) value of zero is a circular orbit. And, the remaining three satellite orbits are of elliptical corresponding to the eccentricity (e) values 0.5, 0.75 and 0.9.

Mean Anomaly

For a satellite, the point which is closest from the Earth is known as Perigee. Mean anomaly (M) gives the average value of the angular position of the satellite with reference to perigee.

If the orbit is circular, then Mean anomaly gives the angular position of the satellite in the orbit. But, if the orbit is elliptical, then calculation of exact position is very difficult. At that time, Mean anomaly is used as an intermediate step.

Argument of Perigee

Satellite orbit cuts the equatorial plane at two points. First point is called as descending node, where the satellite passes from the northern hemisphere to the southern hemisphere. Second point is called as ascending node, where the satellite passes from the southern hemisphere to the northern hemisphere.

Argument of perigee (ω) is the angle between ascending node and perigee. If both perigee and ascending node are existing at same point, then the argument of perigee will be zero degrees

Argument of perigee is measured in the orbital plane at earth’s center in the direction of satellite motion.

Inclination

The angle between orbital plane and earth’s equatorial plane is known as inclination (i). It is measured at the ascending node with direction being east to north. So, inclination defines the orientation of the orbit by considering the equator of earth as reference.

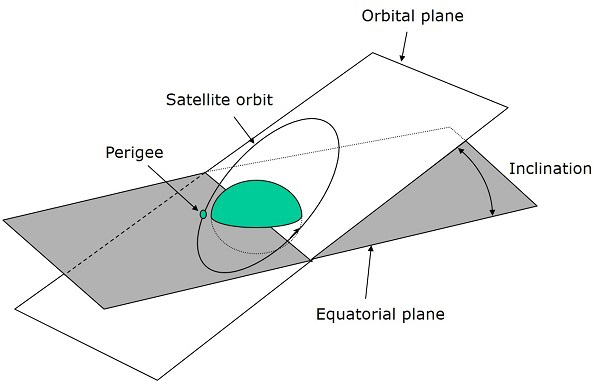
There are four types of orbits based on the angle of inclination.

Equatorial orbit − Angle of inclination is either zero degrees or 180 degrees.
Polar orbit − Angle of inclination is 90 degrees.
Prograde orbit − Angle of inclination lies between zero and 90 degrees.
Retrograde orbit − Angle of inclination lies between 90 and 180 degrees.

Right Ascension of Ascending node

We know that ascending node is the point, where the satellite crosses the equatorial plane while going from the southern hemisphere to the northern hemisphere.

Right Ascension of ascending node (Ω) is the angle between line of Aries and ascending node towards east direction in equatorial plane. Aries is also called as vernal and equinox.

Satellite’s ground track is the path on the surface of the Earth, which lies exactly below its orbit. The ground track of a satellite can take a number of different forms depending on the values of the orbital elements.

Orbital Equations

In this section, let us discuss about the equations which are related to orbital motion.

Forces acting on Satellite

A satellite, when it revolves around the earth, it undergoes a pulling force from the earth due to earth’s gravitational force. This force is known as Centripetal force (F₁) because this force tends the satellite towards it.

Mathematically, the Centripetal force (F₁) acting on satellite due to earth can be written as

$$F_{1} = \frac{GMm}{R^2} $$

Where,

G is universal gravitational constant and it is equal to 6.673 x 10^-11 N∙m²/kg².
M is mass of the earth and it is equal to 5.98 x 10²⁴ Kg.
m is mass of the satellite.
R is the distance from satellite to center of the Earth.

A satellite, when it revolves around the earth, it undergoes a pulling force from the sun and the moon due to their gravitational forces. This force is known as Centrifugal force (F₂) because this force tends the satellite away from earth.

Mathematically, the Centrifugal force (F₂) acting on satellite can be written as

$$F_{2} = \frac{mv^2}{R} $$

Where, v is the orbital velocity of satellite.

Orbital Velocity

Orbital velocity of satellite is the velocity at which, the satellite revolves around earth. Satellite doesn’t deviate from its orbit and moves with certain velocity in that orbit, when both Centripetal and Centrifugal forces are balance each other.

So, equate Centripetal force (F₁) and Centrifugal force (F₂).

$$\frac{GMm}{R^2} = \frac{mv^2}{R}$$

$$= > \frac{GM}{R} = v^2$$

$$= > v = \sqrt{\frac{GM}{R}}$$

Therefore, the orbital velocity of satellite is

$$v = \sqrt{\frac{GM}{R}}$$

Where,

G is gravitational constant and it is equal to 6.673 x 10^-11 N∙m²/kg².
M is mass of the earth and it is equal to 5.98 x 10²⁴ Kg.
R is the distance from satellite to center of the Earth.

So, the orbital velocity mainly depends on the distance from satellite to center of the Earth (R), since G & M are constants.