- Satellite Communication Tutorial
- Satellite Communication - Home
- Introduction
- Orbital Mechanics
- Kepler’s Laws
- Earth Orbit Satellites
- Look Angles & Orbital Perturbations
- Launching
- Subsystems
- AOC Subsystem
- TTCM Subsystem
- Power & Antenna Subsystems
- Transponders
- Earth Segment Subsystems
- Examples of Earth Stations
- Link Budget
- Multiple Access Techniques
- Satellite Services
- Global Positioning System
- Satellite Communication Resources
- Quick Guide
- Useful Resources
- Discussion
Satellite Communication - Kepler’s Laws
We know that satellite revolves around the earth, which is similar to the earth revolves around the sun. So, the principles which are applied to earth and its movement around the sun are also applicable to satellite and its movement around the earth.
Many scientists have given different types of theories from early times. But, only Johannes Kepler (1571-1630) was one of the most accepted scientist in describing the principle of a satellite that moves around the earth.
Kepler formulated three laws that changed the whole satellite communication theory and observations. These are popularly known as Kepler’s laws. These are helpful to visualize the motion through space.
Kepler’s First Law
Kepler’s first law states that the path followed by a satellite around its primary (the earth) will be an ellipse. This ellipse has two focal points (foci) F1 and F2 as shown in the figure below. Center of mass of the earth will always present at one of the two foci of the ellipse.
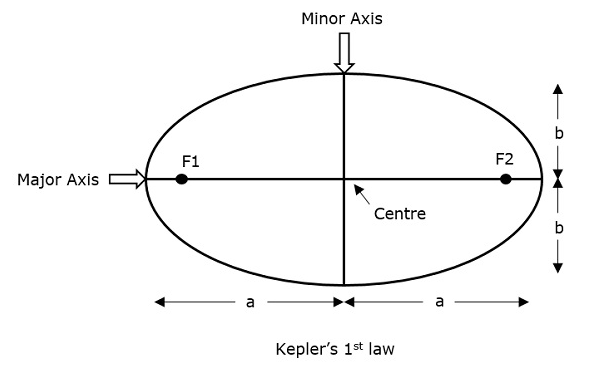
If the distance from the center of the object to a point on its elliptical path is considered, then the farthest point of an ellipse from the center is called as apogee and the shortest point of an ellipse from the center is called as perigee.
Eccentricity "e" of this system can be written as −
$$e = \frac{\sqrt{a^2 - b^2}}{a}$$
Where, a & b are the lengths of semi major axis and semi minor axis of the ellipse respectively.
For an elliptical path, the value of eccentricity (e) is always lie in between 0 and 1, i.e. $0$ < $e$ < $1$, since a is greater than b. Suppose, if the value of eccentricity (e) is zero, then the path will be no more in elliptical shape, rather it will be converted into a circular shape.
Kepler’s Second Law
Kepler’s second law states that for equal intervals of time, the area covered by the satellite will be same with respect to center of mass of the earth. This can be understood by taking a look at the following figure.
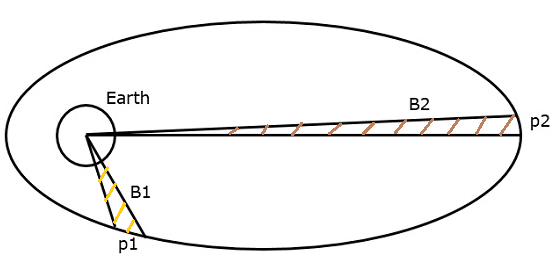
Assume, the satellite covers p1 and p2 distances in the same time interval. Then, the areas B1 and B2 covered by the satellite at those two instances are equal.
Kepler’s Third Law
Kepler’s third law states that, the square of the periodic time of an elliptical orbit is proportional to the cube of its semi major axis length. Mathematically, it can be written as follows −
$$T^2\:\alpha\:a^3$$
$$=> T^2=\left(\frac{4\pi ^2}{\mu }\right) a^3$$
Where, $\frac{4\pi^2}{\mu}$ is the proportionality constant.
$\mu$ is Kepler’s constant and its value is equal to 3.986005 x 1014m3 /sec2
$$1 = \left(\frac{2\pi}{T}\right)^2\left(\frac{a^2}{\mu}\right)$$
$$1 = n^2\left(\frac{a^3}{\mu}\right)$$
$$=> a^3 = \frac{\mu}{n^2}$$
Where, ‘n’ is the mean motion of the satellite in radians per second.
Note − A satellite, when it revolves around the earth, undergoes a pulling force from the earth, which is gravitational force. Similarly, it experiences another pulling force from the sun and the moon. Therefore, a satellite has to balance these two forces to keep itself in its orbit.