Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Resistance and Impedance in an AC Circuit
Resistance in an AC Circuit
Consider the circuit diagram, containing an AC sinusoidal voltage source and an unknown passive element (K). The element K will be a resistance, only if the voltage across it and the current flowing through it, are in phase with each other.
Explanation
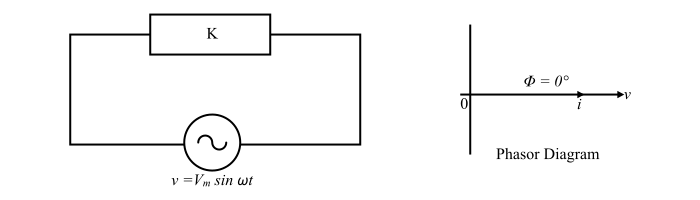
Let the equation for alternating voltage is
$$\mathrm{v=V_{m}\sin\omega\:t\:\:\:...(1)}$$
As a result of this voltage, an alternating current i will flow through the element. Now, the applied voltage has to overcome the drop in the element only, i.e.
$$\mathrm{v=i\times\:k}$$
$$\mathrm{\Rightarrow\:i=\frac{v}{k}=\frac{V_{m}\sin\omega\:t}{k}\:\:\:...(2)}$$
The value of current will be maximum, when sin(ωt) = 1.
$$\mathrm{\therefore\:I_{m}=\frac{V_{m}}{K}}$$
Thus, the equation (2) becomes,
$$\mathrm{i=I_{m}\sin\omega\:t\:\:\:...(3)}$$
It is clear from the eqns. (1) and (3) that the applied voltage and resulting current are in phase with each other. Therefore, the unknown element is resistance, i.e.
$$\mathrm{K=R\:\:\:...(4)}$$
Impedance in an AC Circuit
If an AC circuit containing both resistive and reactive components, then the total opposition offered by the circuit in the flow of electric current is known as impedance of the AC circuit.
It is denoted by letter ‘Z’ and measured in ohms (Ω).
Mathematically, the impedance is expressed as,
$$\mathrm{Impedance,Z=R+jX\:\:\:...(5)}$$
Case 1 – Impedance of a Series R-L Circuit
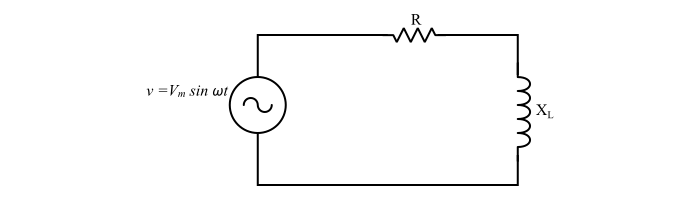
$$\mathrm{Z=R+jX_{L}=R+j\omega\:L\:\:\:...(6)}$$
Case 2 – Impedance of a Series R-C Circuit
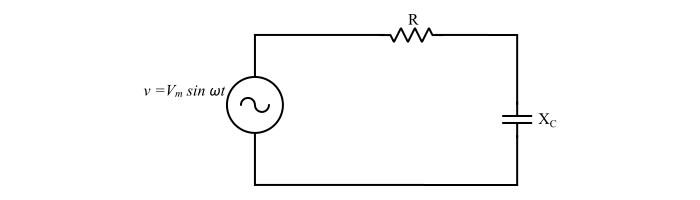
$$\mathrm{Z=R+jX_{C}=R-j\frac{1}{\omega\:C}\:\:\:...(7)}$$
Case 3 – Impedance of a Series RLC Circuit
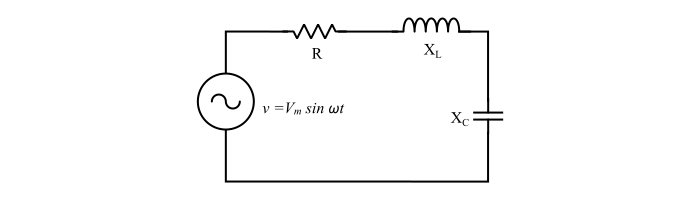
$$\mathrm{Z=R+j(X_{L}-X_{C})=R+j(\omega\:L-\frac{1}{\omega\:C})\:\:\:...(8)}$$
Case 4 – Impedance in a Parallel AC Circuit
In case of a parallel AC circuit, the impedance being given in terms of admittance, i.e.
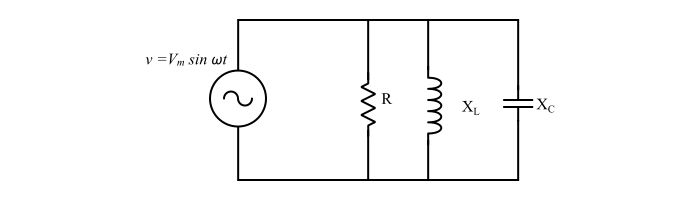
$$\mathrm{Impdance=\frac{1}{Admittance}}$$
$$\mathrm{\Rightarrow\:Z=\frac{1}{Y}=\frac{1}{G+jB}\:\:\:....(9)}$$
Where,
G = 1/R, is called conductance
B = 1/X, is called susceptance
2K+ Views
