How to Calculate Equivalent Resistance (Series & Parallel Circuit Examples)

In electrical and electronic circuits, resistance or electrical resistance is defined as the amount of friction in the flow of electric current (or electric charge) offered by the conductor material. The electric circuit element that is used to introduce the electrical resistance in the circuit is called resistor. The resistor is a passive circuit element that controls the flow of current through a circuit, and coverts the extra amount of electrical energy into heat. Sometimes, we do not have a resistor of desired resistance that is required in the circuit. For this reason, we connect two or more resistor in a particular manner to obtain a desired resistance in the circuit.

In this tutorial, we will understand what the equivalent resistance is, how to determine the equivalent resistance of resistors when they are connected in series or parallel or series and parallel. We will also discuss the numerical examples on each of the three combinations for better understanding of the concept.

How to Calculate Equivalent Resistance in Series?

A combination of resistors in which they are connected end-to-end in a chain fashion, and provides only one path for the flow of electric current, it is called series connection of resistors, or simply resistors in series.

In order to understand the calculation of equivalent resistance in series, consider N-resistor namely R₁, R₂, R₃,…R_N connected in series as shown in Figure-1. Let, the total voltage across the combination is V volts, and I is the total current through the combination. It should note that the current I is common to all resistors.

According Ohm’s law, we have,

$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N}=IR_{N}}$$

Also,

$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$

$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$

$$\mathrm{\Rightarrow V=I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$

But,

$$\mathrm{\frac{V}{I}=R_{eq}}$$

Therefore,

$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$

Hence, when a number of resistors connected in series, then the equivalent resistance of the series combination of resistances can be simply calculated by adding all the resistances.

Special Case − When N-resistors of same resistance value, say R, are connected in series, then their equivalent resistance is calculated by,

$$\mathrm{R_{eq}=N\times R}$$

Where, N is the total number of resistors combined in series.

Here is a list of all the important points that you should note about the series combination of resistors −

• The equivalent resistance of series combination is simply the sum of all resistances.

• The equivalent resistance of the series combination of resistors is always greater than the largest resistance present in the combination.

• The current through all the resistances in series is the same.

• The voltage drop across each resistance is different and depends upon the value of the resistance.

• The resistors are connected in series to divide a voltage into multiple smaller voltage values.

How to Calculate Equivalent Resistance in Parallel?

The combination of resistors in which the one end of all resistors is joined to a common point and the other end of all resistors is joined to another common point so that the number of resistors and number current paths are equal, it is called parallel combination of resistors.

Now, to understand the process of calculating the equivalent resistance of parallel combination of resistors, consider N-resistors connected in parallel as shown in figure-2. From Figure-2, it is clear that the voltage across all the resistors is the same and equals to V volts, but the current through each resistor is different depending the resistance value.

According to Ohm’s law,

$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}};\: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$

Also,

$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$

$$\mathrm{\Rightarrow I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V}{R_{N}}}$$

$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}} \right )}$$

But,

$$\mathrm{\frac{I}{V}=\frac{1}{R_{eq}}}$$

Therefore,

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$

Hence, when several resistances are connected in parallel, then the reciprocal of the equivalent resistance of the combination is equal to the sum of the reciprocal of individual resistances.

When there are only two resistors connected in parallel, then the equivalent resistance is given by,

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{R_{1}+R_{2}}{R_{1}R_{2}}}$$

$$\mathrm{\therefore R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}}$$

Hence, when two resistors are connected in parallel, then the equivalent resistance of the combination is equal to the product divided by the sum of the two resistances.

Special Case − When all the N-resistors connected in parallel are of same resistance value (say R), then the equivalent resistance of the combination is given by,

$$\mathrm{ R_{eq}=\frac{R}{N}}$$

The following are the important points about the parallel combination of resistors −

• The equivalent resistance of the parallel combination of resistors is less than the smallest resistance in the combination.

• The current through each resistance is different.

• The voltage across all the resistances is the same.

• The parallel combination of resistors acts as a current divider as it divides a single electric current in multiple currents.

Equivalent Resistance of Series-Parallel Combination of Resistors

Sometime, we deal with such electric circuits in which some resistors are connected in series and some others are in parallel. Such combination of resistors is usually referred to as a series-parallel combination of resistors. Figure-3 shows a network of resistors which is having resistors connected in series-parallel combination.

The equivalent resistance of a series-parallel combination of resistors is calculated in the following two steps −

Step 1

Calculate the equivalent resistance of all parallel connected resistors. For the given example, we have,

$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$

Step 2

Calculate the equivalent resistance of the series connected resistors. Thus, for the given example, we have,

$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$

Or

$$\mathrm{ R_{eq}=R_{1}+\left ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$

Numerical Example (1)

Calculate the equivalent resistance of the following resistive network −

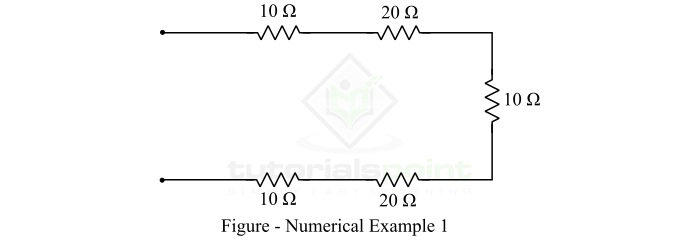
Solution

As it can be observed that in the given network, the resistors are combined in series. Thus, their equivalent resistance will be,

$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$

$$\mathrm{ R_{eq}=70\: \Omega }$$

Numerical Example (2)

Calculate the equivalent resistance of the following resistive network −

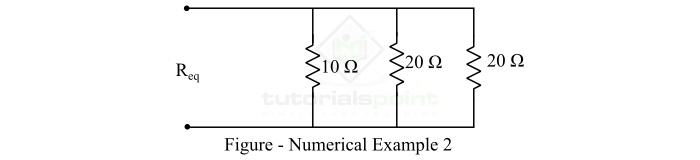
Solution

By inspection, it is clear that the resistors of the network are arranged in parallel. Thus, the equivalent resistance of the combination will be,

$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1}{20} }$$

$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$

$$\mathrm{\therefore R_{eq} =5 \: \Omega } $$

Numerical Example (3)

Calculate the equivalent resistance of the following resistive network.

Solution

As we can see, the network has some resistors in series and some resistors in parallel.

The equivalent resistance of parallel resistances of 10 ohms and 20 ohms is,

$$\mathrm{ R_{cd} =\frac{10\times 20}{10+20} } $$

$$\mathrm{\Rightarrow R_{cd} =\frac{ 200}{30}=6.67\, \Omega }$$

Now, all the resistors are connected in series. Thus, the equivalent resistance of the network is,

$$\mathrm{ R_{eq} =5 + 6.67 + 5=16.67\, \Omega } $$

Conclusion

In this tutorial, we discussed that a set of resistors can be combined in three ways – series, parallel, and series-parallel. In series combination, the equivalent resistance of the combination is equal to the sum of all the resistances. In parallel combination, the reciprocal of the equivalent resistance of the combination is equal to the reciprocal of individual resistances.

The resistances are combined in series and parallel as per the requirements of the circuit or to introduce a desired value of resistance in the circuit, when there is no single resistance available of that particular value of the resistance.