Reflexive Relation

Introduction

A reflexive relation is a relationship between elements of a set where each element is related to the others in the set. As the name implies, every component of the set has a reflection image that is a reflection of itself. In set theory, the reflexive connection is a crucial idea. Since each set is a subset of itself, the relation "is a subset of" on a group of sets is an example of a reflexive relation.

In discrete mathematics, we explore a variety of relations, including reflexive, transitive, symmetric, and others. In this lesson, we will comprehend the idea of reflexive relations and the formula to figure out how many of them there are, along with several instances that have been solved for clarity.

What are relations?

In mathematics, a relationship between the components of two sets is referred to as a relation. They facilitate the mapping of items from one set (the domain) to those from another set (the range), resulting in ordered pairs of the type (input, output).

Assume that X and Y provide two sets. Let x be an element of set X and y be an element of set Y. The collection of all possible ordered pairs (x, y) then yields the cartesian product of X and Y, denoted as $\mathrm{X\:\times\:Y}$. A relation, in other words, states that every input will result in one or more outputs.

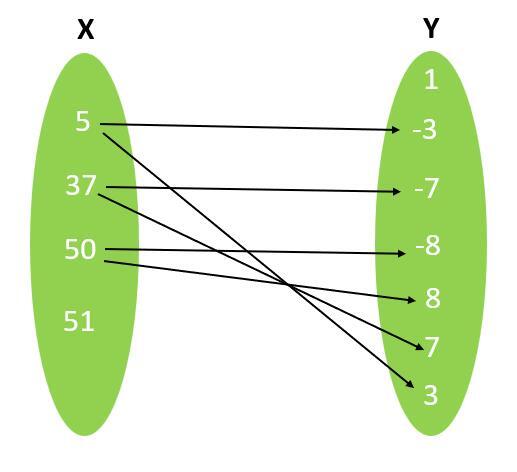
For example − Let's say there are two sets, X = { 5, 37, 50, 51 } and Y ={ 1, -3, -7, -8, 8, 7, 3} respectively. Ordered pairs can be used to indicate a relationship, such as "(x, y) is in the relation R , "R = {(5, -3), (5, 3), (37, -7), (37, 7), (50, -8), (50, 8)}".

Types of Relations

There are eight different categories of relations, including −

• Empty Relation

• Universal Relation

• Identity Relation

• Inverse Relation

• Reflexive Relation

• Symmetric Relation

• Transitive Relation

• Equivalence Relation

Reflexive relation

If we have aRa, or $\mathrm{\lgroup\:a\:,\:a\:\rgroup\varepsilon\:R}$, for every element ‘a ‘ in a binary relation R defined on a set A, then the relation is said to be reflexive. According to this, a relation defined on a set is a reflexive relation if and only if each element of the set is related to itself. R is not a reflexive relation if the set contains a single element that is not connected to itself. R is not reflexive, for instance, if for $\mathrm{b\:\varepsilon\:A}$ and b is not connected to itself (it is shown by $\mathrm{\lgroup\:b\:,\:b\:\rgroup\varepsilon\:R}$ or "not bRb").

$\mathrm{I_{A}\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:\colon\:a\:\varepsilon\:A\:\rbrace}$ is another way to encode a reflexive relation on a set A, where $\mathrm{}$ and R is a relation that is defined on the set A.

Let's look at an illustration. Assume that$\mathrm{}A\:=\:\lbrace\:a\:,\:b\:,\:c\:,\:d\:,\:e\:\rbrace$ and that R is a relation defined on A as $\mathrm{R\:=\:\lbrace\:(a\:,\:a)\:,\:(b\:,\:c)\:,\:(d\:,\:e)\:,\:(c\:,\:e)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:d)\:,\:(e\:,\:e)\:\rbrace}$. Since $\mathrm{\:(a\:,\:a)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:d)\:,\:and\:(e\:,\:e)\:\varepsilon\:R}$, each component of A is related to itself in R, making R a reflexive connection.

On a set with 'n' items, the number of reflexive relations is given by

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

where n is the number of members in the set and N is the number of reflexive relations.

Self related elements

A reflexive relation is one in which each component maps to itself. "Every element is related to itself.“

Let R represent a relation established on set A. Given that R is a reflexive relation,

$$\mathrm{R\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:/\:for\:all\:a\:\varepsilon\:A\:\rbrace}$$

This means that each component of A must be related to itself.

For example, if A= { 2, 4, 6 } and R defined on set A is R = { (2, 2), (4, 4), (6, 6) } When we look at the ordered pairs of R, we find the following associations.

$\mathrm{(2\:,\:2)\:-------->\:2}$ is related to 2

$\mathrm{(2\:,\:2)\:-------->\:4}$is related to 4

$\mathrm{(2\:,\:2)\:-------->\:6}$ is related to 6

That’s how every element of A is related to itself, so all the elements of set A are our self related elements.

Solved Examples

1) If and only if 3a + 7b is divisible by 10, a relation R is defined as aRb on the set of integers Z. Verify R's reflexivity.

Answer −

$\mathrm{3a\:+\:7a\:=\:10a}$, which is divisible by 10, for $\mathrm{a\:\varepsilon\:Z}$.

$\mathrm{\Longrightarrow\:aRa.}$ Given that a can be any element of $\mathrm{Z,\:\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R\:for\:all\:a\:\varepsilon\:Z.}$

R is a reflexive relation as a result.

Hence , If and only if $\mathrm{3a\:+\:7b}$ is divisible by 10 is reflexive, R is defined on Z as aRb

2) A relation R is defined as aRb on the set of natural numbers N if and only if $\mathrm{a\geq\:b}$. Examine R to see if it is a reflexive connection.

Answer −

Because a = a fulfills $\mathrm{a\geq\:a\:for\:all\:a\:\varepsilon\:N}$, the answer is: For $\mathrm{\varepsilon\:N\:,\:a\:=\:a}$.

$\mathrm{\Longrightarrow\:aRa.}$ A is a random component of N, hence $\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R}$ for every N since a is a random component of N.

Therefore, R is reflexive.

3: Take into account the set A where a relation R is defined as 'x R y if and only if $\mathrm{3x\:+\:5y}$ is divisible by 4, for $\mathrm{x\:,\:y\:\varepsilon\:A}$. Establish the fact that R is a reflexive relation on set A.

Answer −

Let's say $\mathrm{x\:\varepsilon\:A}$

Since $\mathrm{3x\:+\:5x\:=\:8x}$ it can be divided by 4.

x R x holds for all x .

As a result, R is reflexive

Conclusion

• In mathematics, a relationship between the components of two sets is referred to as a relation

• Relations facilitate the mapping of items from one set (the domain) to those from another set (the range), resulting in ordered pairs of the type (input, output).

• If we have aRa, or $\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R}$, for every element ‘a’ in a binary relation R defined on a set A, then the relation is said to be reflexive.

• $\mathrm{I_{A}\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:\colon\:a\:\varepsilon\:A}$ is another way to encode a reflexive relation on a set A, where $\mathrm{I_{A}\:\subseteq\:R}$ and R is a relation that is defined on the set A

• R is not a reflexive relation if the set contains a single element that is not connected to itself.

• On a set with 'n' items, the number of reflexive relations is given by

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

where n is the number of members in the set and N is the number of reflexive relations.

FAQs

1. What does "Relation" in math mean?

In mathematics, a relationship between the components of two sets is referred to as a relation. They facilitate the mapping of items from one set (the domain) to those from another set (the range), resulting in ordered pairs of the type (input, output).

2. What is the Relation Equation?

A relation equation is what is created when a relationship is stated as an equation. An illustration of a related equation is $\mathrm{y\:=\:x^{2}}$ . This relationship's graph will look like a parabola

3. How Is the Number of Reflexive Relations Calculated?

On a set with 'n' items, the number of reflexive relations is given by

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

where n is the number of members in the set and N is the number of reflexive relations.

4. What does the mathematical concept of Reflexive Relation mean?

If we have aRa, or $\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\:\varepsilon\:R}$, for every element a A in a binary relation R defined on a set A, then the relation is said to be reflexive. According to this, a relation defined on a set is a reflexive relation if and only if each element of the set is related to itself.

5. How do Irreflexive and Reflexive Relationships Differ?

If every member of the set is related to itself a binary relation on A is said to be reflexive. If at least one element of a set A is not connected to itself, a relation R defined on that set is said to be irreflexive.