Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find the Number of Reflexive Relations on a Set using C++
In this article, we will explain the approaches to find the number of reflexive relations on a set. In this problem, we are given with number n, and on a set of n natural numbers, we must determine the number of reflexive relations.
Reflexive Relation − A relation in a set A is called reflexive if ( a, a ) belongs to R for every 'a' belongs to set A. For example −
Input : x = 1
Output : 1
Explanation : set = { 1 }, reflexive relations on A * A :
{ { 1 } }
Input : x = 2
Output : 4
Explanation : set = { 1,2 }, reflexive relations on A * A :
{ ( 1, 1 ) , ( 2, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ), ( 2, 1 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 2, 1 ) }Hence, a relation is reflexive if: (a, a) ∈ R ∀ a ∈ A.
Approach to Find the Solution
This number of reflexive relations on an element set can be solved by formula 2n2−n. This general formula is generated by calculating the number of reflexive relations of integers.
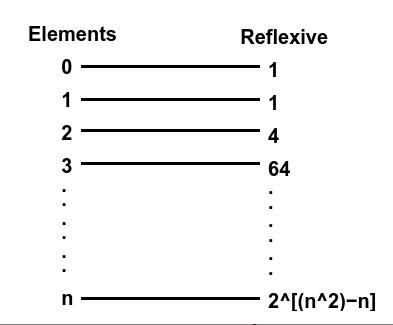
Example
#include <iostream>
using namespace std;
int countReflexive(int n){
int ans = 1 << (n*n - n);
return ans;
}
int main(){
int n ;
cin >> n ; // taking input n from the user using std cin.
int result = countReflexive(n); // calling function to calculate number of reflexive relations
cout << "Number of reflexive relations on set: " << result ; // printing the answer
return 0;
}Output
Number of reflexive relations on set: 1
Explanation of the Above Program
This program is simple to understand as we are just taking input from the user and putting it into the formula 2n2−n, and we are using the left shift "<< "operator for calculating the formula, Time complexity of this code is O(1) which is getting slow as size of n increases.
Conclusion
In this article, we solve a problem to find the Number of Reflexive Relations on a Set. We discussed the simple approach to solve the given problem as a formula to calculate the number of reflexive relations is derived by mathematicians.
We also learned the C++ program for this problem by which we found the solution with a Time complexity of O(1). We can write the same program in other languages such as C, java, python, and other languages.
375 Views
