Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to check existence of edge length limited paths in Python
Suppose we have one undirected weighted graph with n nodes using one edgeList, where edgeList[i] has three parameters (u, v, w) denotes there is a path from u to v whose distance is w. We also have another query array where query[i] has (p, q, lim). This query is trying to ask whether there is a path (direct or via some other node) from p to q whose distance is less than lim. We have to return an array holding True/False results for each query.
So, if the input is like
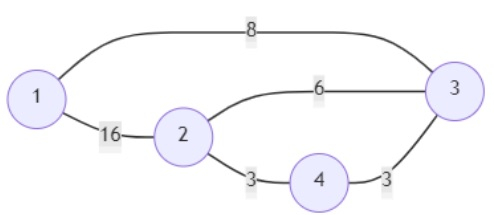
then the output will be [True, False, True]. Because to go from 1 to 4 we can follow path 1 -> 3 - > 4 with cost 11, second one is false because we cannot go from 2 to 3 using less than 3, and last one is true because we can go from 1 to 2 using path 1 -> 3 -> 2 with cost 14 which is less than 15.
To solve this, we will follow these steps −
parent := a list from 0 to n
rank := a list of size n+1 and fill with 0
Define a function find() . This will take parent, x
if parent[x] is same as x, then
return x
parent[x] := find(parent, parent[x])
return parent[x]
Define a function union() . This will take parent, a, b
a := find(parent, a)
b := find(parent, b)
if a is same as b, then
return
if rank[a] < rank[b], then
parent[a] := b
otherwise when rank[a] > rank[b], then
parent[b] := a
otherwise,
parent[b] := a
rank[a] := rank[a] + 1
From the main method do the following −
sort edgeList based on weight parameters
res := an array with number of queries and fill with 0
queries := a list of pair (i, ch) for each index i and value ch from queries
sort queries based on limit parameters
ind := 0
for each index i triplet (a, b, w) in queries, do
while ind < size of edgeList and edgeList[ind, 2] < w, do
union(parent, edgeList[ind, 0])
ind := ind + 1
res[i] := find(parent, a) is same as find(parent, b)
return res
Example
Let us see the following implementation to get better understanding
def solve(n, edgeList, queries):
parent = [i for i in range(n+1)]
rank = [0 for i in range(n+1)]
def find(parent, x):
if parent[x] == x:
return x
parent[x] = find(parent, parent[x])
return parent[x]
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
if a == b:
return
if rank[a] < rank[b]:
parent[a] = b
elif rank[a] > rank[b]:
parent[b] = a
else:
parent[b] = a
rank[a] += 1
edgeList.sort(key = lambda x: x[2])
res = [0] * len(queries)
queries = [[i, ch] for i, ch in enumerate(queries)]
queries.sort(key = lambda x: x[1][2])
ind = 0
for i, (a, b, w) in queries:
while ind < len(edgeList) and edgeList[ind][2] < w:
union(parent, edgeList[ind][0], edgeList[ind][1])
ind += 1
res[i] = find(parent, a) == find(parent, b)
return res
n = 4
edgeList = [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3),]
queries = [(1,4,12),(2,3,3),(1,2,15)]
print(solve(n, edgeList, queries))Input
4, [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3)],[(1,4,12),(2,3,3),(1,2,15)]
Output
[True, False, True]
108 Views
