Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find k-length paths on a binary tree in Python
Suppose we have a binary tree which contains unique values and we also have another value k, we have to find the number of k-length unique paths in the tree. The paths can go either from parent to child or from child to parent. We will consider two paths are different when some node appears in one path but not the other.
So, if the input is like
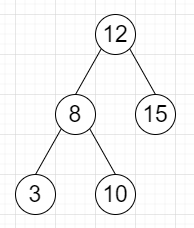
k = 3, then the output will be 4, as the paths are [12,8,3], [12,8,10], [8,12,15], [3,8,10].
To solve this, we will follow these steps−
Define a function dfs() . This will take node
if node is null, then
return a list with 1 and k-1 number of 0s
left := dfs(left of node)
right := dfs(right of node)
for i in range 0 to K, do
ans := ans + left[i] * right[K - 1 - i]
res := a list of size K of 0s
res[0] := 1, res[1] := 1
for i in range 1 to K - 1, do
res[i + 1] := res[i + 1] + left[i]
res[i + 1] := res[i + 1] + right[i]
return res
From the main method, do the following−
ans := 0
dfs(root)
return ans
Let us see the following implementation to get better understanding −
Example
class TreeNode: def __init__(self, data, left = None, right = None): self.data = data self.left = left self.right = right class Solution: def solve(self, root, K): def dfs(node): if not node: return [1] + [0] * (K-1) left = dfs(node.left) right = dfs(node.right) for i in range(K): self.ans += left[i] * right[K - 1 - i] res = [0] * K res[0] = res[1] = 1 for i in range(1, K - 1): res[i + 1] += left[i] res[i + 1] += right[i] return res self.ans = 0 dfs(root) return self.ans ob = Solution() root = TreeNode(12) root.left = TreeNode(8) root.right = TreeNode(15) root.left.left = TreeNode(3) root.left.right = TreeNode(10) print(ob.solve(root, 3))
Input
root = TreeNode(12) root.left = TreeNode(8) root.right = TreeNode(15) root.left.left = TreeNode(3) root.left.right = TreeNode(10) 3
Output
4
187 Views
