Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find number of restricted paths from first to last node in Python
Suppose we have one undirected weighted connected graph. The graph has n nodes and they are labelled from 1 to n. A path from start to end is a sequence of nodes like [z0, z1, z2, ..., zk] here z0 is start node and zk is end node and there is an edge between zi and zi+1 where 0 <= i <= k-1. The distance of a path is the sum of the weights values on the edges of the path. Let dist(x) denotes the shortest distance from node n and node x. A restricted path is a special path that also satisfies that dist(zi) > dist(zi+1) where 0 <= i <= k-1. So, we have to find the number of restricted paths from node 1 to node n. If the answer is too large then return answer modulo 10^9 + 7.
So, if the input is like
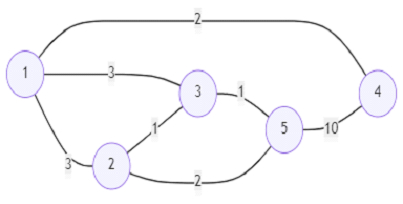
then the output will be 3 because there are three restricted paths (1,2,5), (1,2,3,5), (1,3,5).
To solve this, we will follow these steps −
graph := adjacency list of the graph made from given edge list
paths := an array of size (n+1) and filled with 0
paths[n] := 1
dists := an array of size (n+1) and filled with -1
q := a queue, and insert (0, n) initially
while q is not empty, do
(dist, node) := front element of q and remove it from q
if dists[node] is not same as -1, then
go for next iteration
dists[node] := dist
for each adjacent node v and weight w of graph[node], do
if dists[v] is same as -1, then
insert (dist + w, v) into q
otherwise when dists[v] < dists[node], then
paths[node] := paths[node] + paths[v]
if node is same as 1, then
return paths[node] mod 10^9+7
return 0
Example
Let us see the following implementation to get better understanding −
from collections import defaultdict from heapq import heappop, heappush def solve(n, edges): graph = defaultdict(dict) for u, v, w in edges: graph[u][v] = w graph[v][u] = w paths = [0] * (n+1) paths[n] = 1 dists = [-1] * (n+1) q = [(0, n)] while q: dist, node = heappop(q) if dists[node] != -1: continue dists[node] = dist for v, w in graph[node].items(): if dists[v] == -1: heappush(q, (dist + w, v)) elif dists[v] < dists[node]: paths[node] += paths[v] if node == 1: return paths[node] % (10**9 + 7) return 0 n = 5 edges = [(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)] print(solve(n, edges))
Input
5,[(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]
Output
3
174 Views
