C++ Program to Find Maximum Number of Edge Disjoint Paths

According to the problem statement, we have a directed graph and two vertices that are source s and destination/target t. Our task is to determine the maximum number of edge-disjoint paths that can be found from vertex s to vertex t. If two paths do not share any edge, then it is known as an edge-disjoint.

A directed graph is a digraph where edges have a specific direction. They point from one vertex to another.

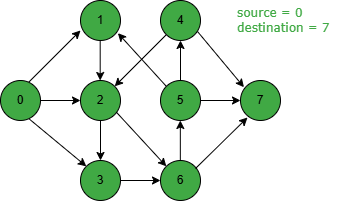
There can be a maximum two-edge disjoint path from source 0 to destination 7 in the above graph. The two edge-disjoint points highlighted below in red and blue colors are 0-1-2-6-7 and 0-3-6-5-7.

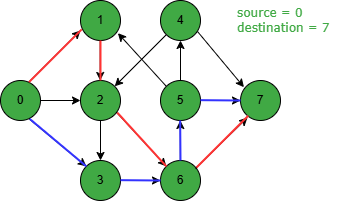
It's important to note that paths may be different but the maximum number is the same. For example, in the above diagram possible set of paths is 0-2-6-7 and 0-3-6-5-7.

C++ Program to Find Maximum Number of Edge Disjoint Paths

In the following C++ example, we create a program to find a maximum number of edge-disjoint paths:

#include <iostream>
#include <climits>
#include <cstring>
#include <queue>

#define n 7
using namespace std;

// Function to check if there is a path from source 's' to target 't'
bool bfs(int g[n][n], int s, int t, int par[]) {
   bool visit[n];
   // Mark all nodes as unvisited initially
   memset(visit, 0, sizeof(visit));
   queue < int > q;
   q.push(s);
   visit[s] = true;
   // Source has no parent
   par[s] = -1;

   while (!q.empty()) {
      int u = q.front();
      q.pop();

      // Check adjacent nodes of 'u'
      for (int v = 0; v < n; v++) {
         // If the node is unvisited and has a positive edge capacity
         if (visit[v] == false && g[u][v] > 0) {
            q.push(v);
            // Store parent node
            par[v] = u;
            visit[v] = true;
         }
      }
   }
   // If destination is reached, return true
   return (visit[t] == true);
}

// Function to find the maximum number of edge-disjoint paths from 's' to 't'
int findDisPath(int G[n][n], int s, int t) {
   int u, v;
   int g[n][n];

   // Create a copy of the original graph
   for (u = 0; u < n; u++) {
      for (v = 0; v < n; v++)
         g[u][v] = G[u][v];
   }

   // Array to store the path
   int par[n];
   int max_flow = 0;

   while (bfs(g, s, t, par)) {
      int path_flow = INT_MAX;

      // Find minimum capacity along the path found by BFS
      for (v = t; v != s; v = par[v]) {
         u = par[v];
         path_flow = min(path_flow, g[u][v]);
      }

      // Update residual capacities along the path
      for (v = t; v != s; v = par[v]) {
         u = par[v];
         g[u][v] -= path_flow;
         g[v][u] += path_flow;
      }

      max_flow += path_flow;
   }

   return max_flow;
}

int main() {
   int g[n][n] = {
      {0, 6, 7, 1},
      {0, 0, 4, 2},
      {0, 5, 0, 0},
      {0, 0, 19, 12},
      {0, 0, 0, 17},
      {0, 0, 0, 0}
   };

   // Define source and destination nodes
   int s = 0, d = 3;
   cout << "There exist maximum " << findDisPath(g, s, d) <<
      " edge-disjoint paths from " << s << " to " << d;

   return 0;
}

Following is the output of the above code:

There exist maximum 3 edge-disjoint paths from 0 to 3