Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program for centered nonagonal number in C++
Given with a value ‘n’ and the task is to generate the centered nonagonal number for n and centered nonagonal series till n and display the results.
What is centered nonagonal number?
Centered nonagonal number contains the nonagonal layers formed by the dots and one corresponding dot in the center.
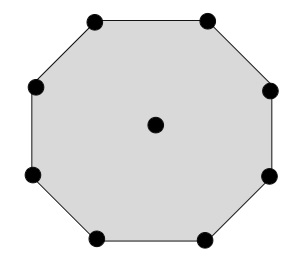
Given above is the figure of centered nonagonal number š2.It can be calculated using the formula −
$$Nc(n)=\frac{(3n-2)(3n-1)}{2}$$
Input
number: 20
Output
centered nonagonal number : 1711
Input
number: 10
Output
centered nonagonal series : 1 10 28 55 91 136 190 253 325 406
Algorithm
Start Step 1→ declare function to calculate centered nonagonal number int calculate_number(int num) return (3 * num - 2) * (3 * num - 1) / 2 Step 2→ declare function to calculate centered nonagonal series int calculate_series(int num) Loop For int i = 1and i <= num and i++ Print (3 * i - 2) * (3 * i - 1) / 2 End Step 3→ In main() Declare int num = 20 Call calculate_number(num) Declare num = 10 Call calculate_series(num) Stop
Example
#include <bits/stdc++.h>
using namespace std;
//calculate centered nonagonal number
int calculate_number(int num){
return (3 * num - 2) * (3 * num - 1) / 2;
}
int calculate_series(int num){
for (int i = 1; i <= num; i++){
cout << (3 * i - 2) * (3 * i - 1) / 2;
cout << " ";
}
}
int main(){
int num = 20;
cout<<"centered nonagonal number : "<<calculate_number(num)<<endl;
num = 10;
cout<<"centered nonagonal series : ";
calculate_series(num);
return 0;
}Output
If run the above code it will generate the following output −
centered nonagonal number : 1711 centered nonagonal series : 1 10 28 55 91 136 190 253 325 406
Updated on: 13-Aug-2020
42 Views
Advertisements