Centered Tridecagonal Number

The problem statement states that we need to print the N-th centred Hexadecagon numbers for any positive number N.

Tridecagonal numbers are the numbers that represent a tridecagon in itself. A tridecagon in mathematics is a polygon which has 13 sides.

A centred tridecagonal numbers are the numbers that can be represented in the form of a dot in the centre followed by other dots surrounding it in successive layers of tridecagon which is nothing but a 13-sided polygon.

Let’s understand the concept of centred tridecagonal numbers better with the figures.

The first centred tridecagonal number can just be represented with a dot in the centre. Therefore, the first centred tridecagonal number is 1.

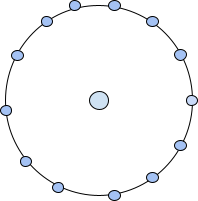
The second centred tridecagonal number can be represented as a dot in the centre followed by a tridecagon surrounding it. Therefore, the second centred tridecagonal number is 14.

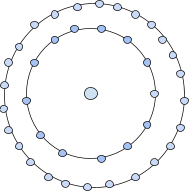
The third-centred tridecagonal is represented as a dot in the centre followed by a tridecagon surrounding it and a successive layer of tridecagon surrounding it.

Therefore the number will be 1+13+26=40.

Following the same pattern the next centred tridecagonal numbers can be found out. Using the concept of centred tridecagonal numbers, the first few centred tridecagonal numbers are 1, 14, 40, 79, 131, 196, 274, 365, 469, 586…..

So in this problem we will be given any positive number N and we need to print the value of the centred tridecagonal number corresponding to the value of N.

Example

INPUT: 5

OUTPUT : 131

INPUT: 8

OUTPUT : 365

Let’s see the algorithm that we will use in this problem to solve it.

Algorithm

There is always a pattern which is followed in such problems. We need to figure out that pattern. Every centred tridecagonal number is represented in the form of dot in the centre surrounded by the successive layers of the tridecagon. The successive layers of the tridecagon are 13, 26, 39, 52……

If we closely observe the successive layers of the tridecagon, we can see that it is an A.P. with a common difference of 13. We can say that the N-th centred tridecagonal number is the sum of 1 and sum of the sequence of successive layers of the tridecagon till N starting with 0.

Let’s understand this better with the illustrations below.

The sequence of successive layers of the tridecagon starting with 0 is 0, 13, 26, 39, 52….

The first centred tridecagonal number is 1 which can be represented as 0+1.

The second centred tridecagonal number is 14 which can be represented as 0+13+1.

The 5th centred tridecagonal number is 131 which can be expressed as sum of successive layers of tridecagon starting with 0 up to 5, and 1.

0+13+26+39+52+1= 131.

From the above examples, we can conclude that the N-th centred tridecagonal number is sum of 1 and sum of the A.P. up to N terms whose first term is 0 and common difference is 13. We can express the formula for N-th centred tridecagonal number as −

$$\mathrm{(centred\:tridecagonal)n\:=\:sum\:of\:N\:terms\:of \:A.P.\:+\:1}$$

$$\mathrm{(centered\:tridecagonal)_N\:=\:\frac{N}{2}(2a\:+\:(N-1)d)\:+1}$$

Where, a= first term of the A.P. which is 0

d= common difference of the A.P. which is 13

$$\mathrm{(centred\:tridecagonal)_N\:=\:N-th\:centred\:tridecagonal\:number}$$

After putting the values in the above formula, it can be written as

$$\mathrm{(centred\:tridecagonal)_N\:=\:(\frac{13N}{2}(N-1))+1}$$

$$\mathrm{(centred\:tridecagonal)_N\:=\:\frac{13N(N-1)}{2}+1}$$

Every centred tridecagonal number can be expressed in the form $\mathrm{(\frac{13N(N-1)}{2})+1}$.

We will be using this formula to calculate the N-th centred tridecagonal number in our approach.

Approach

The step-by-step explanation of the approach that we will use to solve the problem −

• Initialise a function to calculate the N-th centred tridecagonal number.

• Use the formula derived in the algorithm section to find the N-th number and store it in any variable.

• Return the variable and print the value stored in it which will be our output.

Example

The implementation of the approach in C++ −

#include <iostream>
#include <bits/stdc++.h>

//function to calculate N-th centred tridecagonal number
long long int CTn(int N){
   long long int ans= ((13 * N * (N-1))/2) + 1; //store the N-th value
   
   return ans; //return the value
}
using namespace std;

int main(){
   int N=12;
   cout<<N<<"-th centred tridecagonal number is : "<<CTn(N)<<endl; //to print the N-th centred tridecagonal number
   N=17;
   cout<<N<<"-th centred tridecagonal number is : "<<CTn(N)<<endl;
   return 0;
}

Output

12-th centred tridecagonal number is : 859
17-th centred tridecagonal number is : 1769

Time-Complexity : O(1) , since constant time is taken to perform the operation.

Space Complexity : O(1) , no extra space is taken.

Conclusion

This is how we can solve the above problem using the formula that we derived from observing the pattern followed in sequence of centred tridecagonal number to print the N-th centred tridecagonal number in C++.

I hope you find this article to clear the concepts of the problem.