Centered Dodecagonal Number

A figurative number that depicts a dodecagon is called a dodecagonal number. The Centered Dodecagonal number is represented by a dot in the centre and other dots encircling it in the successive dodecagonal (i.e. a 12-sided polygon) layers.

Centered Dodecagonal number can be better explained with the below figure.

For n=1, only a single dot will be there in the centre. So the output will be 1.

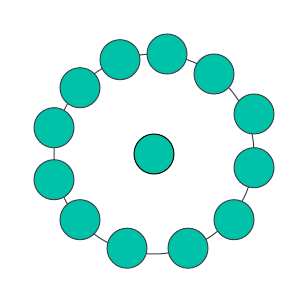
For n=2, a single dot in the centre followed by a dodecagon encircling it. Thus, the total number of dots will be 13. So the next centred dodecagonal number will be 13.

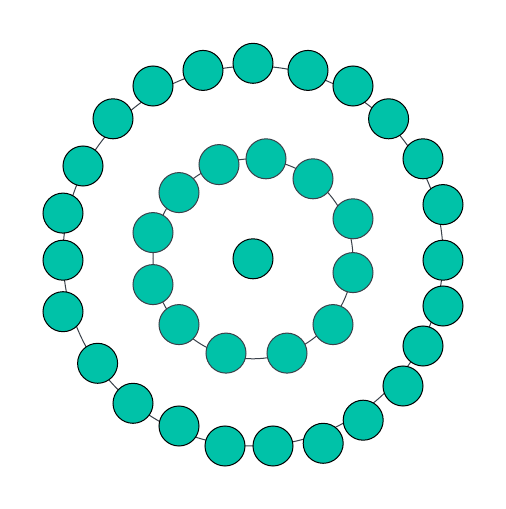
For n=3, there will be a single dot in the centre followed by a dodecagon encircling it which will be further encircled by the next successive dodecagon layer which will consist of 24 dots. Thus, the total number of dots will be 37 which will be the next centred dodecagonal number.

Similarly for every positive number n, this will be followed. With reference to this the first few dodecagonal numbers will be 1, 13, 37, 73, 121, 181…..

In this problem, we will be given any positive number n and we need to print the nth centred dodecagonal number.

For example,

INPUT − 2

OUTPUT − 13

INPUT − 5

OUTPUT − 121

Below is the algorithm to solve this problem.

Algorithm

To calculate the nth centred dodecagonal number, we need to figure out the pattern that is being followed in the problem.

According to the concept of centred dodecagonal numbers, it is represented by a dot in the centre followed by the successive dodecagon layers. The successive dodecagon layers are 12, 24, 36, 48…. If we closely observe the pattern, it is forming an A.P. with a common difference of 12.

As the first few sequences of centred dodecagonal numbers are 1, 13, 37, 73…. which is nothing but the sum of the dodecagon layers and a dot in the centre.

If we consider the sequence of successive dodecagon layers starting with 0 we can understand it better.

0, 12, 24, 36, 48.
For n=1, the centred dodecagonal number is 1 which is 0+1.
For n=2, the centred dodecagonal number is 13 which is 0+12+1.
For n=3, the centred dodecagonal number is 37 which is 0+12+24+1.

From here we can consider that the nth centred dodecagonal number is nothing but the sum of A.P. of n terms starting with 0 and the common difference is 12 and 1.

So the formula for the nth centred dodecagonal number can be,

$$\mathrm{CDn= sum\:of\:n\:terms\:of\:A.P.(a=0\:and\:d=12)\:+1}$$

$$\mathrm{CD_n\:=\:\frac{n}{2}(2a\:+\:(n-1)d)\:+1}$$

Here,$\mathrm{CD_n}$ is the nth centred dodecagonal number

a is the first term of the A.P. i.e. 0

d is the common difference of A.P. which is 12

Further the formula can be written as,

$$\mathrm{CD_n\:=\:\frac{12n}{2}(n-1)\:+\:1}$$

$$\mathrm{CD_n\:=\:6n(n-1)\:+\:1}$$

We will use the above formula to calculate the nth centred Dodecagonal number in our approach.

Approach

• To solve this problem, we simply make a function to calculate the nth centred dodecagonal number.

• We will use the above derived formula to calculate the nth centred dodecagonal number for any n positive number.

• Return the calculated value which will be our desired output.

Example

Below is the implementation of the above approach in C++ −

#include <iostream>
#include<bits/stdc++.h>

using namespace std;

//function to calculate the nth centred dodecagonal number
int CDn(int N){
   int ans= 6 * N * (N-1) + 1; //used to store nth centred dodecagonal number value
   
   return ans; //return the answer
}
int main(){
   int N=8;
   cout<<CDn(N)<<endl;
   
   N=6;
   cout<<CDn(N)<<endl;
   
   N=12;
   cout<<CDn(N)<<endl;
   
   return 0;
}

Output

337
181
793

Time Complexity : O(1), since constant time is taken.

Space Complexity : O(1), since we don’t take any extra space.

Conclusion

In this article, we solved the problem to print the nth centred dodecagonal number. We have learned the concept of centred dodecagonal number and derived the formula for the nth number,

I hope you find this article helpful in understanding and clearing all your concepts regarding the problem.