Centered Octagonal Number

The problem statement includes printing the N-th centered octagonal number for some positive integer N, which will be given by the user.

A centered octagonal number is a type of number which can be represented in a pattern of figures. Every centered octagonal number can be represented as a dot in the centre surrounded by the successive layers of an Octagon. An octagon is a type of polygon in geometry which has 8 sides in it. The successive layers of an octagon means that the first layer surrounding the dot in the centre will be an octagon, the second layer surrounding will be a 16-sided polygon followed by a 24-sided polygon and so on.

Since centered octagonal numbers are a type of figurative numbers. Let’s understand these numbers with the help of the figures below.

The first centered octagonal number is just represented as a dot in the centre. Thus, the number is 1.

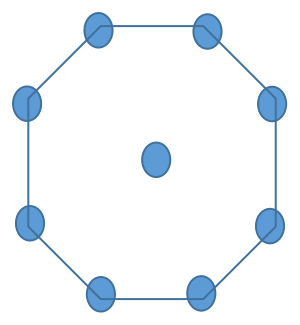
The next centered octagonal number is represented as a dot in the centre surrounded by a layer of an octagon. Thus the number becomes 1+8=9.

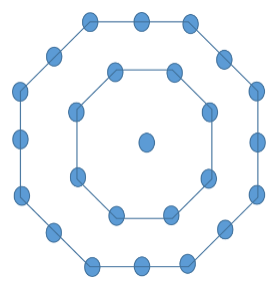
The next centered octagonal number is represented in the form of a figure as a dot in the centre surrounded by 2 successive layers of an octagon i.e 8-sided polygon and 16-sided polygon. Thus the third centered octagonal number is 1+8+16=25.

Similarly the next numbers in the sequence of centered octagonal numbers are represented in terms of figures. Following the pattern of the figures, we can calculate the numbers in the sequence of centered octagonal numbers. The first few numbers in the sequence of centered octagonal numbers are 1, 9, 25, 49, 81, 121, 169, 225, 289…….

In this problem, we will be given any positive integer i.e. N. Our task involves to print the value of centered octagonal number with reference to N i.e. N-th centered octagonal number.

Example −

INPUT : N= 4
OUTPUT : 49

Explanation − The value of N given is 4. The centered octagonal number with reference to N, i.e. 4th centred octagonal number is 49 which can be represented as a dot in the centre surrounded by (N-1) successive layers of an octagon. The 3 successive layers of an octagon are 8, 16, 24. Thus the number is 1+8+16+24=49.

INPUT : N=7
OUTPUT : 169

Explanation − The value of centered octagonal number corresponding to input value of N is 169 represented as a dot in the centre surrounded by (N-1) successive layers of an octagon i.e. 1+8+16+24+32+40+48=169.

Let’s understand the algorithm to calculate the N-th centered octagonal number for any positive value of N using the pattern followed in the figures.

Algorithm

If we observe the pattern followed in figurative representation of any centered octagonal number, we can conclude that it is the sum of (N-1) successive layers of an octagon and 1, where N is the N-th centered octagonal number and 1 represents the dot in the centre.

The successive layers of an octagon are 8, 16, 24, 32, 4To calculate the sum of n terms of an AP with first term, as a and common difference, as d0…… The sequence formed by the successive layers of an octagon is an AP whose first term is 8 (i.e. a=8) and the common difference between every term in the sequence is also 8 (i.e. d=8).

To calculate the sum of n terms of an AP with first term, as a and common difference, as d −

$$\mathrm{S_n = \frac{n}{2}(2*a+(n − 1)d)}$$

where , 𝑆_𝑛 represents sum of first n terms of the AP and a and d are first term and common difference of an AP respectively.

We can use this formula to calculate the sum of first (N-1) terms of the sequence of successive layers of an octagon as it is also an AP to calculate the N-th centered octagonal number.

Therefore, the N-th centered octagonal number can be given by,

$$\mathrm{(Centered \: Octagonal)_N=sum \: of \:(N − 1)successive \: layers \: of \: an \: octagon +1}$$

The sum of (N-1) successive layers of an octagon can be calculated by putting the values in the above formula to calculate sum of first n terms of an AP.

$$\mathrm{(Centered \: Octagonal)_N=\frac {N − 1}{2}(2*a+(N − 2)d)+1}$$

The value of a i.e. first term is 8 and d i.e. common difference is also 8 as the sequence is 8, 16, 24, 32…….

$$\mathrm{(Centered \: Octagonal)_N=\frac {(N − 1)}{2}(16+(N − 2)*8)+1}$$

This expression can be further simplified as,

$$\mathrm{(centered \: octagonal)_N=\frac {8*(N − 1)}{2}(2+N − 2)+1}$$

$$\mathrm{=4N(N − 1)+1}$$

We will use the expression that we derived using the pattern followed in the figurative representation of the centered octagonal numbers to calculate the N-th centered octagonal numbers in our approach to solve the problem.

Approach

The steps to follow to implement the formula for the N-th centered octagonal numbers in our approach are as follows −

• To calculate the N-th centered octagonal number for any input value of N, create a function.

• Initialise a variable named ans to store the value of N-th number which will be our required answer. Make sure the variable is of long long data type to store the values of centered octagonal numbers for larger values of N.

• Using the formula, 4𝑁(𝑁 − 1) + 1 we will calculate the centered octagonal number for N and store it in ans.

• Return the variable, which is the output we require.

The C++ code for the approach −

Example

//C++ code to  print the N-th centered octagonal number
//for any positive value of N
#include <bits/stdc++.h>
using namespace std;

//function to calculate the N-th centered octagonal number for given value of N
long long number(int N){

   //long long data type is used to store larger values of N-th number
   long long ans; //to store the N-th centered octagonal number
   ans = 4*N*(N-1)+1; //using the formula 4N(N-1)+1 to calculate the number
   return ans; //return the value stored in ans
}

int main(){
   int N;
   N=14;
   
   //calling the function
   cout<<"The centered octagonal number for N="<<N<<" is "<<number(N)<<endl;   
   N=25;
   cout<<"The centered octagonal number for N="<<N<<" is "<<number(N)<<endl; 

   return 0;
}

Output

The centered octagonal number for N=14 is 729
The centered octagonal number for N=25 is 2401

Time Complexity − O(1) , because the expression took constant time to calculate the N-th centered octagonal number.

Space Complexity − O(1) , because we didn’t use any extra space while solving the problem.

Conclusion

The concepts of centered octagonal numbers and the pattern followed in their figurative representation are being discussed in the article. We derived an expression following the pattern of figures of every centered octagonal number which we used in our approach in order to solve the above problem within constant time and space in C++.

I hope you have cleared all the concepts of the centered octagonal numbers after reading this article.