Centered Pentadecagonal Number

The problem includes printing the N-th centered pentadecagonal number for any input number N.

A centered pentadecagonal number is a number that can be represented in the form of a figure with a dot in the centre and surrounded by successive layers of the pentadecagon i.e. 15-sided polygon. Here the successive layers of the pentadecagon depict that the first layer surrounding the dot in the centre will be 15-sided polygon, the next layer will be 30-sided polygon followed by a 45-sided polygon and so on.

We can understand the concept of centered pentadecagonal with the below figures.

The first centered pentadecagonal number is being represented with a dot in the centre. Therefore, the first number will be 1.

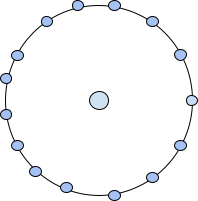
The next centered pentadecagonal number can be represented as a dot in the centre followed by a surrounding layer of pentadecagon (15-sided polygon). Therefore, the second centered pentadecagonal number will be 15+1=16.

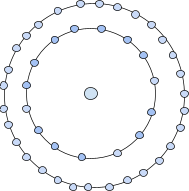
The third centred pentadecagonal number is 46 as it is represented in the form of figure with a dot in the centre surrounded by successive layers of pentadecagon. The successive layers of the pentadecagon suggest the first layer will be of 15-sided polygon and the second layer will be of 30-sided polygon.

We can calculate the successive centred pentadecagonal numbers following the same pattern. The first few centred pentadecagonal numbers calculated by following the pattern in figures are 1, 16, 46, 91, 151, 226, 316, 421, 541…….

We will be given any positive integer N corresponding to which we need to print the N-th centred pentadecagonal number.

Example−

INPUT : N=5
OUTPUT : 151

Explanation − The 5th centred pentadecagonal number is 151 represented as a dot in the centre surrounded by four successive layers of a pentadecagon which sums to 1+15+30+45+60=151.

INPUT : N=9
OUTPUT : 541

Explanation − The 9th centred pentadecagonal number is 541.

Let’s look out to the algorithm to figure out the N-th centred pentadecagonal number.

Algorithm

We need to observe the pattern followed in the sequence of centred pentadecagonal number. Every N-th centred pentadecagonal number when represented in the form of figure is surrounded by (N-1) successive layers of a pentadecagon. The sequence of successive layers of pentadecagon is 15, 30, 45, 60, 75…..

The first centred pentadecagonal number is surrounded by 0 layers of pentadecagon as it is just represented as a dot in the centre. So we can say that the N-th centred pentadecagonal number is, sum of (N-1) successive layers of the pentadecagon + 1.

Since the sequence of the successive layers of the pentadecagon forms an A.P. with the first term as a=15 and common difference as d=15. So the N-th centred pentadecagonal number can be calculated as −

$$\mathrm{(centered \: pentadecagonal)_N=sum \: of \: (N − 1)successive \: layers \: of \: pentadecagon + 1}$$

$$\mathrm{sum \: of \: N \: ters \: of \: AP =\frac{N}{2}(2*a+(N − 1)d)}$$

Where, a= first term of AP

$$\mathrm{d= common \: difference \: of \: AP}$$

Using the formula for calculating N-th centred pentadecagonal number,

$$\mathrm{(centered \: pentadecagonal)_N=\frac{(N − 1)}{2}(2*15+(N − 2)*15)+1}$$

$$\mathrm{=\frac{15*(N − 1)}{2}(2+N − 2)+1}$$

$$\mathrm{=\frac{15*N*(N − 1)}{2}+1}$$

This is the formula to get any N-th centred pentadecagonal number derived using simple mathematics. We will use this formula in our approach to the problem.

Approach

The steps to follow to apply the formula to calculate the N-th centred pentadecagonal number in C++ −

• We will create a function to calculate N-th centred pentadecagonal number.

• Initiate a variable named ans as long long int to store the N-th centred pentadecagonal number for larger values of N.

• Use the derived formula in the algorithm to calculate the number.

• Print the calculated number which will be our required output.

The C++ code for the approach −

Example

//C++ code to print the N-th centred pentadecagonal number
#include<bits/stdc++.h>
using namespace std;

//function to give the N-th centred pentadecagonal number
long long int Nth_number(int N){
   long long int ans= (15 * N * (N-1))/2 + 1; //to store N-th number
    
   return ans; //return the N-th number
}
int main(){
   int N;
   N=12;
   cout<<"The N-th centred pentadecagonal number is "<<Nth_number(N)<<endl; //calling the function
   N=19;
   cout<<"The N-th centred pentadecagonal number is "<<Nth_number(N)<<endl;
}

Output

The N-th centred pentadecagonal number is 991
The N-th centred pentadecagonal number is 2566

Time Complexity − O(1) , constant time is taken to calculate the N-th number.

Space Complexity − O(1) , we have not used any extra space.

Conclusion

The concept behind the centred pentadecagonal number was discussed in the article. We figured out the formula to calculate the N-th centred pentadecagonal number for any positive number N using the pattern followed in the sequence of centred pentadecagonal numbers. We came up with an efficient approach to print the N-th centred pentadecagonal number in C++ using the derived formula.

I hope your concepts related to the topic have been cleared after reading this article.