Centered nonadecagonal number

The problem statement includes printing of the N-th centered nonadecagonal number for any positive value of N.

A centered nonadecagonal numbers are numbers which are represented in a particular pattern of figure. This number can be represented in a figure as a dot in the centre surrounded by the successive layers of the nonadecagon.

A nonadecagon is a type of polygon in mathematics which has 19 sides in it. The successive layers of the nonadecagon suggests that the first layer surrounding the dot in the centre will be 19 sided polygon followed by 38 sided polygon and so on.

These numbers can be better understood with the figures below.

The first number is represented as just a dot in the centre. Thus the first centered nonadecagonal number is 1.

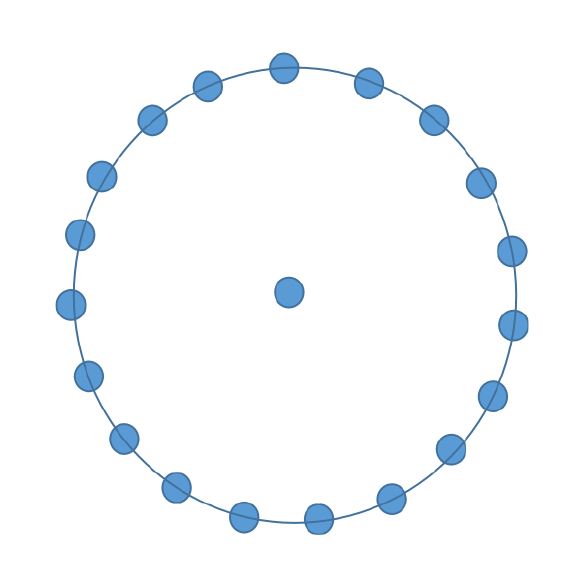
The next number is represented as a dot in the centre surrounded by a nonadecagon. Thus the number will be 1+19=20.

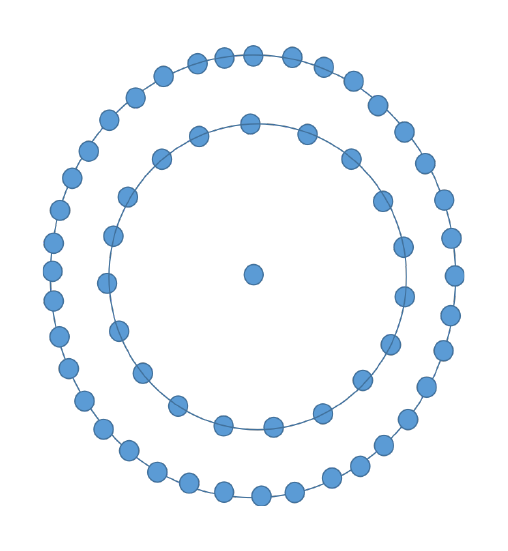
The next number is represented as the dot in the centre surrounded by the successive layers of nonadecagon i.e 19-sided polygon and 38-sided polygon making the number to be 1+19+38=58.

Similarly all the next numbers in the sequence of the centered nonadecagonal numbers follow the same pattern. We could get any centered nonadecagonal number following the pattern of figures. The first few numbers of the sequence of the centered nonadecagonal numbers are 1, 20, 58, 115, 191, 286, 400, 533……

The positive integer N will be the user input and we need to print the value of the centered nonadecagonal number corresponding to the value of N in this problem.

Example −

INPUT : N=5
OUTPUT : 191

Explanation − The value of N given is 5. The 5th number in the sequence of the centered nonadecagonal numbers is 191 which is represented as a dot in the centre surrounded by 4 successive layers of the nonadecagon.

INPUT : N=8
OUTPUT : 533

Explanation − The value of centered nonadecagonal number corresponding to N is 533 i.e. 8th centered nonadecagonal number. It is represented as a dot in the centre surrounded by 7 successive layers of the nonadecagon.

Let’s understand the algorithm to print the N-th centered nonadecagonal number by following the pattern in the numbers.

Algorithm

Observing the pattern followed in every centered nonadecagonal number, we can figure out an expression to calculate the N-th centered nonadecagonal number.

It can be clearly seen that every centered nonadecagonal number is the sum of (N-1) successive layers of the nonadecagon + 1, as first number has 0 layers of nonadecagon surrounding the dot in the centre whereas second number has a layer surrounding the dot in the centre, third number has 2 successive layers of the nonadecagon surrounding the dot in the centre and so on.

The first few successive layers of the nonadecagon are 19, 38, 57, 76, 95….

The sequence of successive layers of the nonadecagon is forming an AP with the first term as 19 (i.e. a=19) and common difference as 19 (i.e. d=19). We can say that every N-th centered nonadecagonal number is 1 + sum of (N-1) successive layers of the nonadecagon, observing the pattern of figures followed.

(centered nonadecagonal)_𝑁 = sum of (𝑁 − 1) 𝑠𝑢𝑐𝑐𝑒𝑠𝑠𝑖𝑣𝑒 𝑙𝑎𝑦𝑒𝑟𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑛𝑜𝑛𝑎𝑑𝑒𝑐𝑎𝑔𝑜𝑛 + 1

The sum of (N-1) successive layers of the nonadecagon can be calculated using the formula for the sum of n terms of AP since successive layers of the nonadecagon forms an AP.

(centered nonadecagonal)_𝑁 = sum of (𝑁 − 1) 𝑠𝑢𝑐𝑐𝑒𝑠𝑠𝑖𝑣𝑒 𝑙𝑎𝑦𝑒𝑟𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑛𝑜𝑛𝑎𝑑𝑒𝑐𝑎𝑔𝑜𝑛 + 1

The sum of (N-1) successive layers of the nonadecagon can be calculated using the formula for the sum of n terms of AP since successive layers of the nonadecagon forms an AP.

$$\mathrm{S_n=\frac{n}{2}(2a+a(n−1)d)}$$

Calculating the sum of (N-1) successive layers of the nonadecagon using the above formula, where a=19 and d=19.

$$\mathrm{(centered \: nonadecagonal)_N=\frac{(N−1)}{2}(2*19+(N−2)*19)+1}$$

The expression can be further simplified as,

$$\mathrm{(centered \: nonadecagonal)_N=\frac{19*(N−1)}{2}(2+N−2)+1\=\frac{19*N*(N−1)}{2}+1}$$

Every number in the sequence of centered nonadecagonal numbers can be represented in the form of above expression where N is the Nth centered nonadecagonal numbers.

We will use this expression$\mathrm{(\frac{19*N*(N−)}{2}+1)}$in our approach to get the N-th centered nonadecagonal number for any value of N greater than 0.

Approach

The steps to follow to implement the expression in our approach in order to get the N-th centered nonadecagonal number −

• Create a function to calculate the N-th centered nonadecagonal number.

• Create a variable to store the value of the N-th number. The variable should be of long long datatype to store the values of centered nonadecagonal number for larger values of N.

• Use the formula, $\mathrm{\frac {19*N*(N−1)}{2}+1}$ to get the value of N-th centered nonadecagonal number and store it in the variable created.

• Return the value and print the value as this value will be our required output.

The C++ code for the approach −

Example

//C++ code to print the N-th centered nonadecagonal number
#include <bits/stdc++.h>

using namespace std;

//function to calculate the N-th centered nonadecagonal number for any value of N
long long number(int N){
   //to store the N-th number
   long long n = (19*N*(N-1)/2)+1; //using the formula 19*N*(N-1)2+1
   return n; //return the N-th centered nonadecagonal number
}
int main(){
   int N;
   N=11;
   //calling the function
   cout<<"The N-th centered nonadecagonal number is "<<number(N)<<endl;
   N=20;
   cout<<"The N-th centered nonadecagonal number is "<<number(N)<<endl;
   return 0;
}

Output

The N-th centered nonadecagonal number is 1046
The N-th centered nonadecagonal number is 3611

Time Complexity − O(1) , because constant time is required to calculate the N-th centered nonadecagonal number.

Space Complexity − O(1) , because no extra space is taken.

Conclusion

We discussed the centered nonadecagonal numbers and their figurative representation in this article. We derived a formula to represent any N-th centered nonadecagonal number using the pattern followed by each number, which we used in our approach in C++ to print the N-th centered nonadecagonal number.

I hope all your concepts have been cleared after reading this article.