Lumped Capacitance Analysis using Python

When an object at very high temperature is suddenly dropped in a cooler liquid and if it is assumed that the conductive resistance of the solid is very small in comparison to the surrounding convective resistance then the heat transfer analysis is called as lumped capacitance analysis (as shown in the figure given below). Here, we treat the system as a lump. In that case, we can assume that the rate of change of internal energy of lump will be equal to the heat interaction with the surrounding fluid.

Mathematically, this can be written as −

$$\mathrm{pcV\frac{\partial T}{\partial t} \: = \: − hA(T \: − \: T_{\infty}) \: \dotso\dotso \: (1)}$$

$$\mathrm{\frac{\partial T}{\partial t} \: = \: − \frac{hA}{pcV}(T \: − \: T_{\infty}) \: \dotso\dotso \: (2)}$$

Now the Eq 2 has to be solved to obtain the variation of temperature with time.

If we integrate Eq. 2 with the initial temperature of object $\mathrm{T_{0}}$ to some arbitrary temperature T in time 0 to t then the final answer will be −

$$\mathrm{\frac{T \: − \: T_{\infty}}{T_{0} \: − \: T_{\infty}} \: = \: exp(− \frac{hA}{pcV}t) \: \dotso\dotso \: (3)}$$

Now this equation can be used in the following way −

• If time is required to arrive at some temperature $\mathrm{T_{f}}$ −

$$\mathrm{t \: = \: − \frac{pcV}{hA}In(\frac{T_{f} \: − \: T_{\infty}}{T_{0} \: − \: T_{\infty}}) \: \dotso\dotso \: (4)}$$

• If temperature is required at some time $\mathrm{t_{f}}$ −

$$\mathrm{T \: = \: T_{\infty} \: + \: (T_{0} \: − \: T_{\infty}) \: \times \: exp (−\frac{hA}{pcV}t_{f}) \: \dotso\dotso \: (5)}$$

Let us demonstrate this with the help of following examples −

Example 1

A steel ball of radius 1 mm is at temperature $\mathrm{1200^{\circ}C}$ is placed in open air having temperature $\mathrm{25^{\circ}C}$. Calculate the time required to cool the ball to arrive at $\mathrm{100^{\circ}C}$. $\mathrm{(k_{b} \: = \: 50 \: W/mK, \: c_{b} \: = \: 500kJ/kgK, \: p_{b} \: = \: 8000kg/m^{3}, \: and \: h_{air} \: = \: 10000W/m^{2}K)}$.

Solution

As time is expected, so we will be using Equation 4.

# lumped capacitance analysis
from pylab import *
#Input Data

T_inf=25
r=1.E-3
T0=1200
Tf=100
k=50
c=500
ρ=8000
h=10000

#Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3

τ0=ρ*c*V/(h*A)

t=-τ0*log((Tf-T_inf)/(T0-T_inf))

print(f't = {round(t,3)} s')

Output

The program output will be −

t = 0.367 s

Example 2

In Example 1, what is the temperature of the ball after 0.1 sec.

Solution

In this case, Eq. 5 has to be solved. Everything will be same except the formula.

# lumped capacitance analysis
from pylab import *

# Input Data
T_inf=25
r=1.E-3
T0=1200
Tf=100
t=0.1

k=50
c=500
ρ=8000
h=10000

# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3

τ0=ρ*c*V/(h*A)

T=T_inf+(T0-T_inf)*exp(-t/τ0)

print(f'T = {round(T,3)} deg. C')

Output

The output will be −

T = 580.031 deg. C

To understand the picture, one should plot the variation of temperature. For that case, Eq. 3 will be used as follows −

Example 3

from pylab import *

# Input Data
T_inf=25
r=1.E-3
T0=1200

k=50
c=500
ρ=8000
h=10000

# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3

# Evaluating time constant

τ0=ρ*c*V/(h*A)

t= linspace(0,1.0,50)
T=T_inf+(T0-T_inf)*exp(-t/τ0)

figure(1,dpi=300)
plot(t,T,'r-o')
xlabel('t (s)')
ylabel('T ($^\circ$C)')
savefig('plot1.jpg')
show()

Output

Here is the plot that shows the variation in temperature −

Numerical Approach

If one wants to follow the numerical approach then you can also do that. Let us use explicit method to solve Eq. 2.

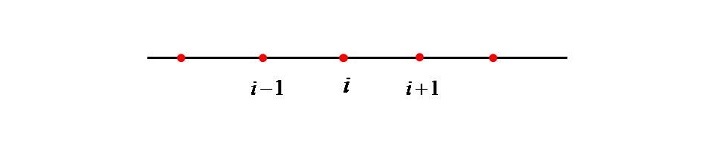
For the grid shown above the Eq. 2 can be discretized (using forward difference) as −

$$\mathrm{\frac{T_{i} \: − \: T_{i − 1}}{\Delta t} \: = \: −\tau_{0}(T_{i} \: − \: T_{\infty})}$$

$$\mathrm{T_{i} \: = \: T_{i − 1} \: − \: \Delta t \: \times \: (T_{i} \: − \: T_{\infty})/\tau_{0} \: \dotso\dotso \: (6)}$$

subscript represent the time step.

We will march in time but in every time step, we will iterate till the solution gets converged.

As at the initial time temperature is known, i.e., 1200 so will start with second time step. First, we will guess the value of temperature at this time step (say 0) then we will solve Eq. 6 and then compare the guess value and the value obtained. If the absolute difference becomes less than the convergence criterion $\mathrm{10^{− 5}}$ then we will move to the next time step. Else, we will set the obtained value of temperature as the guess and again solve equation 6. The process is repeated till the last time step. The program for this is shown below. Where we have also compared the result with the exact analytical value (Eq. 3).

Example

from pylab import *

# Input Data
T_inf=25
r=1.E-3
T0=1200

k=50
c=500
ρ=8000
h=10000

# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3

τ0=ρ*c*V/(h*A)

n=35 # Number of time steps

t = linspace(0,1.0,n)

Δt=1/(n-1)

# initial guess for all time steps
T=zeros(n)

# initial condition
T[0]=T0

# Array of guess
Tg=T.copy()

# Time marching
for i in range(1,n):

   # Iteration loop
   error=1
   
   while error>1.E-5:
      T[i]=T[i-1]-Δt*(T[i]-T_inf)/τ0
      error=abs(T[i]-Tg[i])

      Tg=T.copy()

# Exact solution
T_exact=T_inf+(T0-T_inf)*exp(-t/τ0)
# Data Plotting
figure(2,dpi=300)
plot(t,T,'r-o',label='Numerical')
plot(t,T_exact,'b-o',label='Analytical')
xlabel('t (s)')
ylabel('T ($^\circ$C)')
legend()
savefig('plot2.jpg')
show()

Output

The program output will be as follows −

Data on the basis of which the above plot is generated is shown below −

time       T(analytical)    T(numerical)
0.0         1200.0            1200.0
0.0294      987.6506          967.4051
0.0588      813.6776          780.853
0.0882      671.1455          631.2296
0.1176      554.3722          511.2245
0.1471      458.7025          414.9749
0.1765      380.3226          337.7781
0.2059      316.1076          275.8627
0.2353      263.4978          226.2036
0.2647      220.3958          186.3748
0.2941      185.0833          154.4301
0.3235      156.1526          128.809
0.3529      132.4503          108.2597
0.3824      113.0316          91.7782
0.4118      97.1223           78.5592
0.4412      84.0881           67.957
0.4706      73.4095           59.4535
0.5         64.6608           52.6334
0.5294      57.4932           47.1632
0.5588      51.6209           42.776
0.5882      46.8099           39.2572
0.6176      42.8684           36.4349
0.6471      39.6391           34.1713
0.6765      36.9935           32.3558
0.7059      34.826            30.8997
0.7353      33.0502           29.7319
0.7647      31.5954           28.7952
0.7941      30.4034           28.0439
0.8235      29.4269           27.4414
0.8529      28.6269           26.9581
0.8824      27.9714           26.5705
0.9118      27.4344           26.2596
0.9412      26.9945           26.0103
0.9706      26.634            25.8103
1.0         26.3387           25.6499

Conclusion

In this tutorial, lumped capacitance analysis has been explained and modelled using Python. Both analytical and numerical approaches were discussed.