Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Regression Analysis and the Best Fitting Line using Python
In this tutorial, we are going to implement regression analysis and the best-fitting line using Python programming
Introduction
Regression Analysis is the most basic form of predictive analysis.
In Statistics, linear regression is the approach of modeling the relationship between a scalar value and one or more explanatory variables.
In Machine learning, Linear Regression is a supervised algorithm. Such an algorithm predicts a target value based on independent variables.
More About Linear Regression and Regression Analysis
In Linear Regression / Analysis the target is a real or continuous value like salary, BMI, etc. It is generally used to predict the relationship between a dependent and a bunch of independent variables. These models generally fit a linear equation, however, there are other types of regression as well including higher-order polynomials.
Before fitting a linear model on the data, it is necessary to check if the data points have linear relationships between them. This is evident from their scatterplots. The goal of the algorithm/model is to find the best-fitting line.
In this article, we will explore Linear Regression Analysis and its implementation using C++.
The linear regression equation is in the form of Y = c + mx , where Y is the target variable and X is the independent or explanatory parameter/variable. m is the slope of the regression line and c is the intercept. Since this is a 2-dimensional regression task, the model tries to find the line of best fit during training. It is not necessary that all the points exactly line on the same line. Some of the data points may lie on the line, some scattered around it. The vertical distance between the line and the data point is the residual. This can be either negative or positive based on whether the point lies below or above the line. Residuals are the measure of how well the line fits the data. The algorithm is continuous to minimize the total residual error.
The residual for each observation is the difference between predicted values of y(dependent variable) and observed values of y
$$\mathrm{Residual\: =\: actual\: y\: value\:−\:predicted\: y\: value}$$
$$\mathrm{ri\:=\:yi\:−\:y'i}$$
The most common metric for evaluating linear regression model performance is called root mean squared error, or RMSE. The basic idea is to measure how bad/erroneous the model's predictions are when compared to actual observed values.
So, a high RMSE is “bad” and a low RMSE is “good”
RMSE error is given as
$$\mathrm{RMSE\:=\:\sqrt{\frac{\sum_i^n=1\:(yi\:-\:yi')^2}{n}}}$$
RMSE is the root of the mean of all the squared residuals.
Implementation using Python
Example
# Import the libraries import numpy as np import math import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error # Generate random data with numpy, and plot it with matplotlib: ranstate = np.random.RandomState(1) x = 10 * ranstate.rand(100) y = 2 * x - 5 + ranstate.randn(100) plt.scatter(x, y); plt.show() # Creating a linear regression model based on the positioning of the data and Intercepting, and predicting a Best Fit: lr_model = LinearRegression(fit_intercept=True) lr_model.fit(x[:70, np.newaxis], y[:70]) y_fit = lr_model.predict(x[70:, np.newaxis]) mse = mean_squared_error(y[70:], y_fit) rmse = math.sqrt(mse) print("Mean Square Error : ",mse) print("Root Mean Square Error : ",rmse) # Plot the estimated linear regression line using matplotlib: plt.scatter(x, y) plt.plot(x[70:], y_fit); plt.show()
Output
Mean Square Error : 1.0859922470998231 Root Mean Square Error : 1.0421095178050257
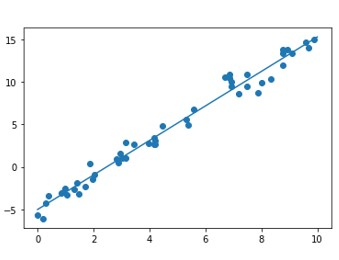
Conclusion
Regression Analysis is a very simple yet powerful technique for predictive analysis both in Machine Learning and Statistics. The idea lies in its simplicity and underlying linear relationships between independent and target variables.
956 Views
