Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Inorder Successor in BST II in C++
Suppose we have a node in a binary search tree, we have to find the in-order successor of that node in the BST. If there is no in-order successor, return null. As we know that the successor of a node is the node with the smallest key greater than value of node.
We will have direct access to the node but not to the root of the tree. Here each node will have a reference to its parent node. Below is the definition for Node −
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
}If the input is like −
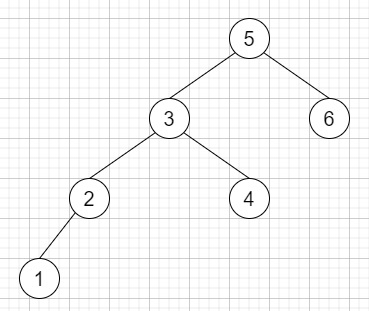
and node is 2, then the output will be 3.
To solve this, we will follow these steps −
if right of node is not null, then −
node := right of node
while left of node is not null, do −
node := left of node
return node
while (parent of node is not null and node is not equal to left of parent of node), do −
node := parent of node
parent of return node
Example
Let us see the following implementation to get a better understanding −
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int val;
Node* left;
Node* right;
Node* parent;
Node(int v, Node* par = NULL){
val = v;
left = NULL;
right = NULL;
parent = par;
}
};
class Solution {
public:
Node* inorderSuccessor(Node* node) {
if (node->right) {
node = node->right;
while (node->left)
node = node->left;
return node;
}
while (node->parent && node != node->parent->left) {
node = node->parent;
}
return node->parent;
}
};
main(){
Solution ob;
Node *root = new Node(5);
root->left = new Node(3, root);
root->right = new Node(6, root);
root->left->left = new Node(2, root->left);
root->left->right = new Node(4, root->left);
root->left->left->left = new Node(1, root->left->left);
cout << (ob.inorderSuccessor(root->left->left))->val;
}Input
Node *root = new Node(5); root->left = new Node(3, root); root->right = new Node(6, root); root->left->left = new Node(2, root->left); root->left->right = new Node(4, root->left); root->left->left->left = new Node(1, root->left->left); (ob.inorderSuccessor(root->left->left))->val
Output
3
285 Views
