Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Preorder Successor of a Node in Binary Tree in C++
In this problem, we are given a binary tree and a node value. Our task is to print the preorder successor of the node.
Binary Tree is a special type of tree in which each root node can have maximum 2 child nodes.
Preorder Traversal is a way to traverse nodes of the tree. In this we will first traverse root node then left child and then the right child.
Preorder successor node is the node that comes next to the node in the preorder traversal of the node.
Let’s take an example to understand the problem
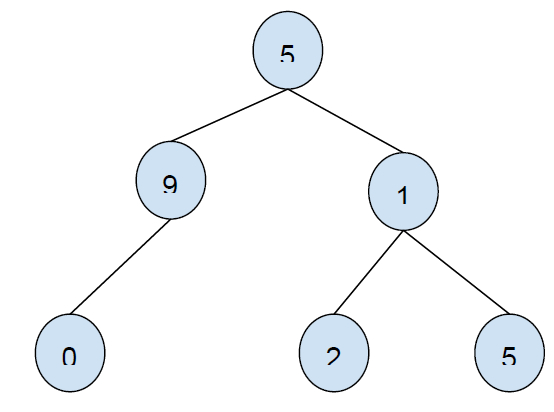
Input: 9 Output 0 Explanation: the preorder traversal of the tree is: 5 9 0 1 2 5. So the preorder successor of 9 is 0.
To solve this problem, a navie approach will be to find the preorder traversal of the binary tree and then print the element that comes after the given number.
A more effective solution will involve checking the position of the given number and then searching for its successor based on positions. So, if the position has a left child, then the preorder successor is left child. If it’s a leaf node but is left child then its sibling node is the preorder successor. If it’s a leaf node and is not left child then we have to move up to its ancestor nodes whose child nodes will be the preorder successor.
The program will make the solution more clear
Example
#include <iostream>
using namespace std;
struct Node {
struct Node *left, *right, *parent;
int key;
};
Node* insertNode(int key){
Node* temp = new Node;
temp->left = temp->right = temp->parent = NULL;
temp->key = key;
return temp;
}
Node* preOrderSuccessorNode(Node* root, Node* n){
if (n->left)
return n->left;
Node *curr = n, *parent = curr->parent;
while (parent != NULL && parent->right == curr) {
curr = curr->parent;
parent = parent->parent;
}
if (parent == NULL)
return NULL;
return parent->right;
}
int main(){
Node* root = insertNode(99);
root->parent = NULL;
root->left = insertNode(4);
root->left->parent = root;
root->left->left = insertNode(18);
root->left->left->parent = root->left;
root->left->right = insertNode(50);
root->left->right->parent = root->left;
root->right = insertNode(26);
root->right->parent = root;
root->right->left = insertNode(5);
root->right->left->parent = root->right;
root->right->right = insertNode(10);
root->right->right->parent = root->right;
Node* preOrder = preOrderSuccessorNode(root, root->left->right);
if (preOrder) {
cout<<"Preorder successor of "<<root->left->right->key<<" is "<<preOrder->key;
} else {
cout<<"Preorder successor of "<<root->left->right->key<<" is NULL";
}
return 0;
}Output
Preorder successor of 50 is 26
482 Views
