
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Replace Each Node in Binary Tree With The Sum Of Its Inorder Predecessor And Successor Using C++
We are given a binary tree, and we need to replace all the elements with the sum of its inorder predecessor and successor. Inorder is a traversed path in a graph that reads in the order of left node - root node - right node. The method adds the elements in left and right nodes of the parent node and replaces the value with the obtained sum.
Suppose we have a tree with the following formation and characters ?
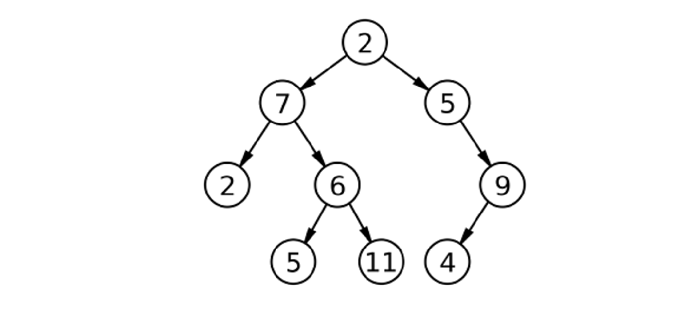
We can find and store the inorder of the tree in an array. After that, we can again do an inorder traversal, but we will replace the element with the indexes in our array this time.
Let us look at some input scenarios ?
Assume the input given as the nodes of binary tree reading, [3 8 15 7 10 3 6 4 9], and the resultant binary tree is obtained as ?
Input: [3 8 15 7 10 3 6 4 9] Result? Before: 3 8 15 7 10 3 6 4 9 After: 8 18 15 25 10 16 7 15 4
Assume another input given as the nodes of binary tree reading, [4 6 7 8 5 3 2 7 1], and the resultant binary tree is obtained as ?
Input: [4 6 7 8 5 3 2 7 1] Result? Before: 8 6 2 5 7 4 7 1 3 After: 6 10 11 9 9 14 5 10 1
Example
Following is the C++ implementation of the above method ?
#include <iostream> #include <vector> using namespace std; class Node { public: int value; Node *left, *right; Node(int value) { this->value = value; left = right = NULL; } }; void solve(Node* root, vector<int>& arr, int& index) { if(root == NULL) return; solve(root->left, arr, index); index++; root->value = arr[index-1] + arr[index+1]; solve(root->right, arr, index); } void storeInOrder(Node* root, vector<int>& arr) { if(root == NULL) return; storeInOrder(root->left, arr); arr.push_back(root->value); storeInOrder(root->right, arr); } void printInorder(Node* root) { if(root == NULL) return; printInorder(root->left); cout << root->value << " "; printInorder(root->right); } int main() { Node* root = new Node(2); root->left = new Node(7); root->right = new Node(5); root->left->left = new Node(2); root->left->right = new Node(6); root->right->right = new Node(9); root->left->right->left = new Node(5); root->left->right->right = new Node(11); root->right->right->left = new Node(4); cout << "Before: "; printInorder(root); cout << "\n"; vector<int> arr; arr.push_back(0); storeInOrder(root, arr); arr.push_back(0); int index = 0; solve(root, arr, index); cout << "After: "; printInorder(root); return 0; }
Output
Before: 2 7 5 6 11 2 5 4 9 After: 7 7 13 16 8 16 6 14 4
Explanation
| Node | Inorder Predecessor | Inorder Successor | New Value |
|---|---|---|---|
| 2(root) | 11 | 5 | 16 |
| 7(root->left) | 2 | 5 | 7 |
| 5(root->right) | 2 | 4 | 6 |
| 2(root->left->left) | 0(not available) | 7 | 7 |
| 6(root->left->right) | 5 | 11 | 16 |
| 9(root->right->right) | 4 | 0(not available) | 4 |
| 5(root->left->right->left) | 7 | 6 | 13 |
| 11(root->left->right->right) | 6 | 2 | 8 |
| 4(root->right->right->left) | 5 | 9 | 14 |
Conclusion
Storing the inorder and then finding the inorder of each element turn by turn is the key. We use the index as a backtrack to find out where the element was when inserted into the array, and then we compute the new in order of the tree. We traverse the tree and each node once, so the time complexity is O(n), and we store each element in the form of inorder, so the space complexity is O(n).

