Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Thevenin’s Theorem and Thevenin Equivalent Circuit
Thevenin’s Theorem is used, where it is desired to determine the current through or voltage across any one circuit element without going through the complex method of solving a set of network equations.
Statement of Thevenin’s Theorem
Any two terminal bilateral linear dc circuit can be replaced by an equivalent circuit consisting of voltage source in series with a resistance, the voltage source being the open circuited voltage across the open circuited load terminals and the resistance being the internal resistance of the source network looking through the open circuited load terminals.
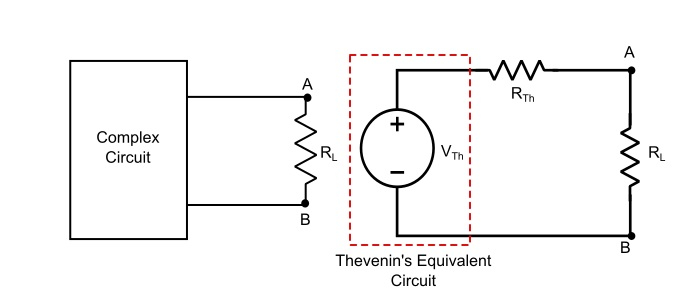
Explanation of Thevenin’s Theorem
Step 1 – Remove the load resistor (RL) and find the open circuited voltage (VOC = VTh) across the open circuited load terminals.
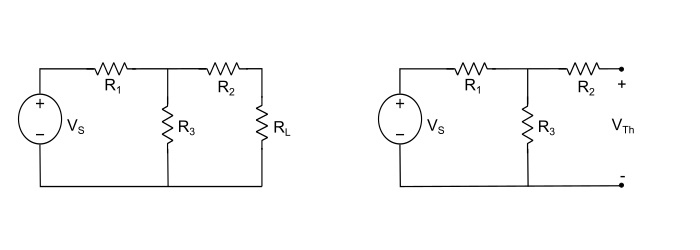
$$\mathrm{\mathit{V}_{rh}=\mathit{IR}_{3}=\mathit{V}_{s}\frac{\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}}$$
Where, I is the current flowing in the closed loop through the resistances R1 and R3.
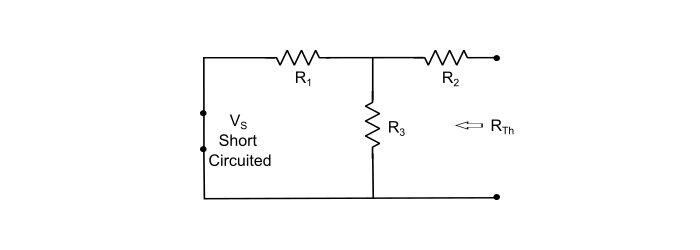
Step 2 - Deactivate the constant sources (for voltage source, remove it by internal resistance and for current source replace the source by open circuit) and find the internal resistance (RTh) looking through the open circuited load terminals.
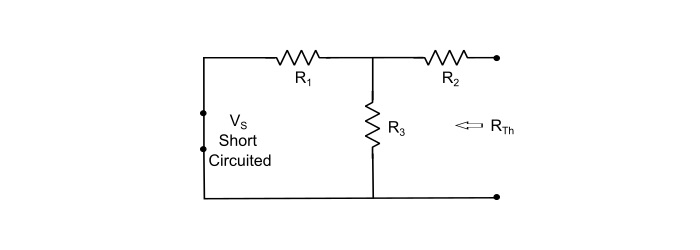
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{R}_{1}\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}+\mathit{R}_{2}}$$
Step 3 Obtain the Thevenin’s equivalent circuit by placing RTh in series with VThh. Reconnect the load resistor (RL) across the load terminals. And, find the current through the load.
Here, the load current (IL) through RL is given by,
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{Th}+\mathit{R}_{L}}}$$
Methods of Finding Thevenin’s Equivalent Resistance (RTh)
For Independent Sources – The RTh of any linear bilateral network containing independent current or voltage sources can be determined by deactivating the sources by their internal resistance i.e., for independent ideal voltage source, deactivate it by shorting it and for independent ideal current source, deactivate it by removing the source. Then find the internal resistance of the network looking through the open circuited load terminals
For the circuits containing dependent sources or independent sources or both
First method Find VTh across the open circuited load terminals. Next, short circuit the load terminals and determine the short circuit current (ISC) through the shorted terminals. The internal resistance or Thevenin’s equivalent resistance is given by,
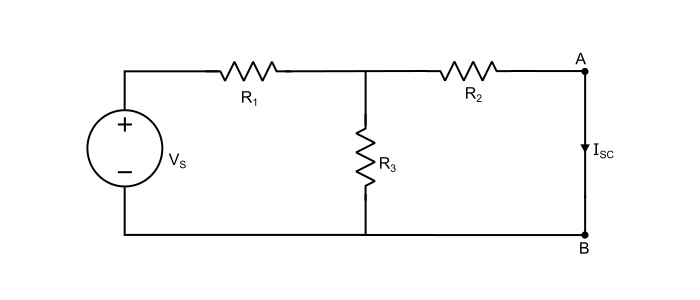
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{rh}}{\mathit{I}_{sc}}}$$
Second Method - Remove the load resistance and apply a DC test voltage (VT) at the open circuited load terminals. Keep the other independent sources deactivated during this time. A direct current (IT) will flow in the circuit from the load terminals due to application of VT. The internal resistance or Thevenin’s equivalent resistance of the source network is obtained as,
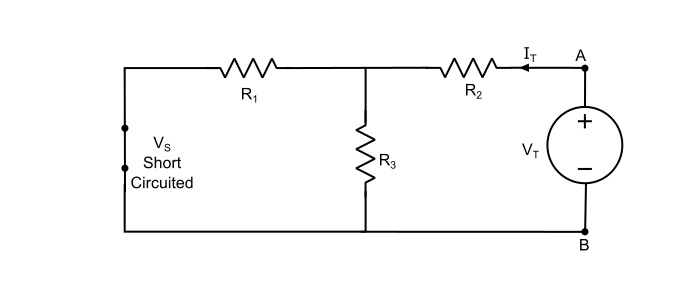
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{T}}{\mathit{I}_{T}}}$$
Numerical Example
Using Thevenin’s Theorem, find the current in 10 Ω resistor in the figure given below. Given that battery has an internal resistance of 2 Ω.
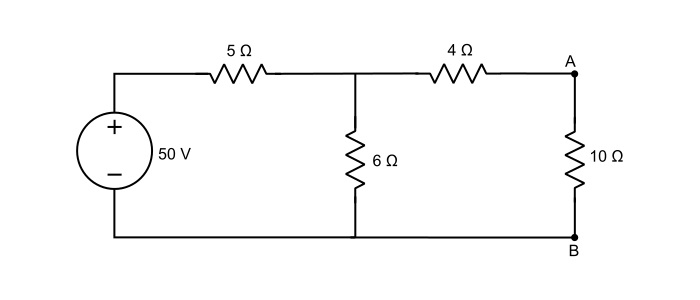
Solution
Step 1 – Remove the load resistance and determine the open circuited voltage (VTh) across the load terminals.
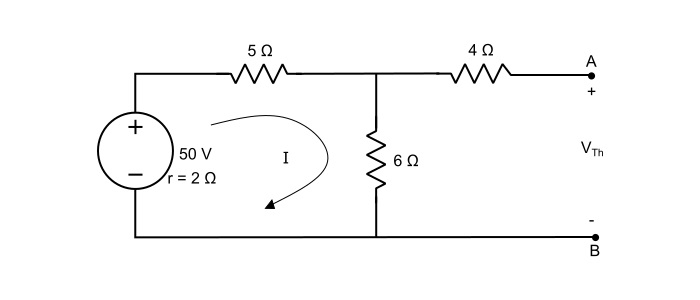
Here, with 10 Ω resistor removed, there is no voltage drop in 4 Ω and the VTh will be the voltage appearing across 6 Ω resistor. Thus,
$$\mathrm{\mathit{I}=\frac{50}{2+5+6}=\frac{50}{13}=3.846\:A}$$
With 10 Ω resistor removed, there is no drop 4 Ω resistor and VTh will be the voltage appearing across 6 Ω resistor. Thus,
$$\mathrm{\mathit{V}_{Th}=\mathit{I}×6=3.846×6=23.076\:V}$$
Step 2 – To find the RTh, deactivate all the independent sources. As,
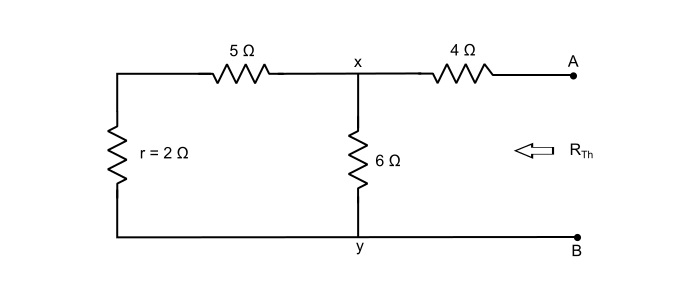
$$\mathrm{\mathit{R}_{xy}=(5+2)||6=\frac{7×6}{7+6}=3.23\:Ω}$$
$$\mathrm{\mathit{R}_{Th}=\mathit{R}_{xy}+4=3.23+4=7.23 \:Ω}$$
Step 3 – Construct the Thevenin’s equivalent circuit and reconnect the load resistance to calculate the load current, as,
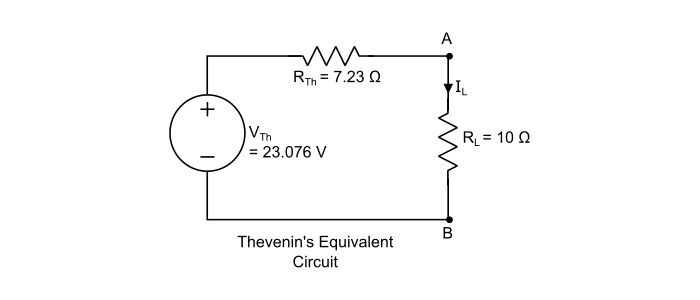
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{rh}+\mathit{R}_{L}}=\frac{23.076}{7.23+10}=1.339\:A}$$
1K+ Views
