Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Electric Traction: Power Output and Energy Output at Driving Axles
Power Output from the Driving Axles
Let,
πΉπ‘ = Tractive effort in Newton
π = Speed of the train in kmph
Since, the power output is defined as the work done per unit time, i.e.,
$$\mathrm{Power\: output,\mathit{P}\mathrm{\: =\: }Rate\: of \: work\: done\mathrm{\: =\: }\frac{Work \: done}{time}}$$
$$\mathrm{\Rightarrow \mathit{P}\mathrm{\: =\: }\frac{Tractive\: effort\times Distance}{Time}\mathrm{\: =\: }Tractive\: effort\times Speed}$$
$$\mathrm{\therefore \mathit{P\mathrm{\: =\: }F_{t}\times V}\: Nm/s}$$
$$\mathrm{\Rightarrow \mathit{P\mathrm{\: =\: }F_{t}\times V}\times \frac{1000}{3600}\, Watts}$$
$$\mathrm{\therefore \mathit{P\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600}}}\: kW\: \cdot \cdot \cdot \left ( 1 \right )}$$
Now, if πΌ is the efficiency of gear transmission, then the power output of motor (or power input to driving axles) is given by,
$$\mathrm{Power\: input,\mathit{P_{i}\mathrm{\: =\: }\frac{F_{t}\times V}{\eta }}\: Watt\: \cdot \cdot \cdot \left ( 2 \right )}$$
$$\mathrm{\Rightarrow \mathit{P_{i}\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600\eta }}}\: kW\: \cdot \cdot \cdot \left ( 3 \right )}$$
Energy Output from the Driving Axles
Assume the run of the electric train according to the simplified trapezoidal speed-time curve.
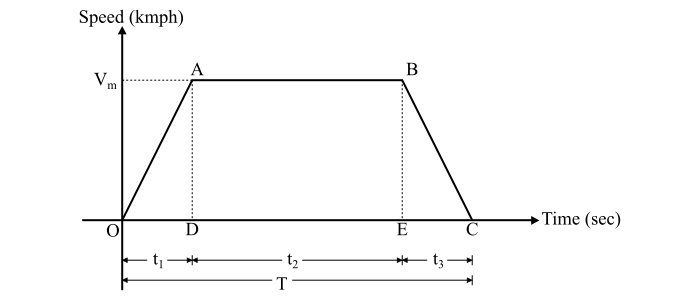
Then, the total energy required for the run (or energy output from driving axles) is given by
$$\mathrm{Total\: energy\mathrm{\: =\: }Energy\: required\: during\: acceleration\mathrm{\: +\: }Energy\: required \: during\: free\: run}$$
$$\mathrm{\Rightarrow Total\: energy\mathrm{\: =\: }Average\: power\: during \: acceleration\times acceleration\: period\mathrm{\: +\: }Average\: power\: during\: free \: run \times duration\: of\: free \: run}$$
From the figure, we have,
$$\mathrm{Total\: energy\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}\times V_{m}}}{\mathrm{3600}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\mathrm{\: +\: }\frac{\mathit{F_{t}^{'}V_{m}}}{3600}\mathrm{\: +\: }\frac{\mathit{t_{\mathrm{2}}}}{3600}\: \: kWh …(4)}$$
Where,
π½π is the maximum speed of train in kmph.
ππ is the tractive effort required during acceleration (in Newton)
ππ′ is the tractive effort required during free run in Newton
π1 is the time of acceleration in seconds
π2 is the duration of free run in seconds
In practice, the energy output from driving axles or total energy required for run is expressed in watt-hours per ton-km, instead of kWh. Therefore,
$$\mathrm{\mathrm{\: =\: }\frac{Energy\: output\: in\: watt\: hours}{Weight\: of\: train\: in\: tons\times Distance \: of\: run\: in\: km} \: \: \: \cdot \cdot \cdot \left ( 5 \right )}$$
The quantity given by equation (5) is known as the specific energy output from the driving axles.
Numerical Example (1)
An electric train weighing 100 tons is to be driven up an incline of 2% at a speed of 35 kmph. If the train resistance at this speed is 1 kg per ton, find the power output from driving axles.
Solution
Given data,
Weight of train,π = 100 tons
Gradient,πΊ = 2%
Specific resistance of train,π = 1 kg per ton
Speed,π = 35 kmph
Therefore, the tractive effort required is,
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }\mathrm{98.1}WG\mathrm{\: +\: }Wrg}} $$
$$\mathrm{\Rightarrow \mathit{F_{t}}\mathrm{\: =\: }98.1\times 100\times 2\mathrm{\: +\: }100\times 1\times 9.81\mathrm{\: =\: }20601\: Newton} $$
$$\mathrm{\therefore Power\: output\: from\: driving\: axles,\: \mathit{P\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600}}}\mathrm{\: =\: }\frac{20601\times 35}{3600}} $$
$$\mathrm{\mathit{P}\mathrm{\: =\: }200.29 \: kW} $$
Numerical Example (2)
Calculate the specific energy output of train whose weight is 100 tons, if maximum speed of 46 kmph and for a given run of 1.5 km and the tractive effort during acceleration is 9810 N and acceleration period is 30 seconds. The tractive effort required during free run is 981 N and the duration of free run is 73 seconds. Assume a trapezoidal speed-time curve.
Solution
Given data,
Maximum speed,ππ = 46 kmph
Distance travelled,π = 1.5 km
Tractive effort during acceleration,πΉπ‘ = 9810 N
Tractive effort during free run,πΉπ‘′ = 981 N
Period of acceleration,π‘1 = 30 sec
Period of free run,π‘2 = 73 sec
Now, the energy output in watt-hours is given by,
$$\mathrm{\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}\times V_{m}}}{\mathrm{3600}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\mathrm{\: +\: }\frac{\mathit{F_{t}^{'}V_{m}}}{3600}\mathrm{\: +\: }\frac{\mathit{t_{\mathrm{2}}}}{3600}}$$
$$\mathrm{\mathrm{\: =\: }\frac{1}{2}\times \frac{9810\times 46}{3600}\times \frac{30}{3600}\mathrm{\: +\: }\frac{981\times 46}{3600}\times \frac{73}{3600}\mathrm{\: =\: }0.5223\mathrm{\: +\: }0.2542\mathrm{\: =\: }0.7765 \: kWh}$$
$$\mathrm{\therefore Energy\: output\: in\: watt\: hours\mathrm{\: =\: }776.5 \, Wh}$$
Thus, the specific energy output is given by,
$$\mathrm{\mathrm{\: =\: }\frac{Energy\: output\: in\: watt\: hours}{Weight\: of\: train\: in\: tons \times Distance \: of \: run\: in\: km}}$$
$$\mathrm{\mathrm{\: =\: }\frac{776.5}{100\times 1.5}\mathrm{\: =\: }5.17\: Whton-km}$$
1K+ Views
