Determination of Specific Energy Output of an Electric Train

Energy output is the energy required for the propulsion of a train, it is mainly for accelerating the train from the rest to maximum velocity (V_m) and the energy required to overcome the gradient and track resistance to motion.

The specific energy output is defined as −

$$\mathrm{Specific\: Energy\: Output\mathrm{\: =\: }\frac{Energy\: output\: in \: watt \: hours}{Weight\: of\: train\: in\: tons\times distance\: of\: run\: in \: km}}$$

The specific energy output is measured in watt-hours per ton-km. The specific energy output is used for comparing the dynamic performances of trains operating to different schedules.

Determination of Specific Energy Output of an Electric Train

Assume the run of the train according to the simplified trapezoidal speed-time curve as shown in the figure.

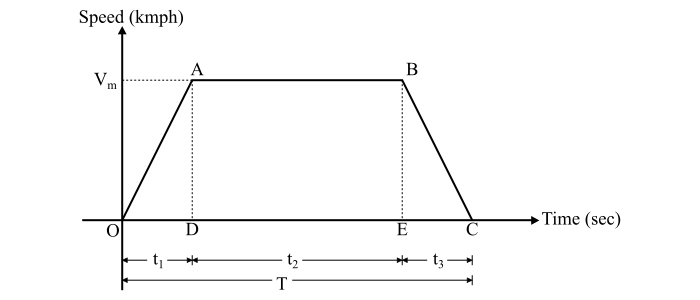
Consider a track having a gradient of G% throughout its run. Then,

Energy output to accelerate the train from rest to a speed 𝑽_𝒎 (say 𝐸₁) −

$$\mathrm{\mathit{E_{\mathrm{1}}}\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}V_{m}}}{3600}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\: kWh}$$

Where, 𝐹_𝑡 is the tractive effort.

$$\mathrm{\mathit{\Rightarrow E_{\mathrm{1}}}\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}V_{m}}}{3600}\times \frac{\mathit{V_{m}}}{3600\alpha }\: kWh}\; \; \left ( \because \mathit{t_{\mathrm{1}}\mathrm{\: =\: }\frac{V_{m}}{\alpha }} \right )$$

$$\mathrm{\mathit{\because F_{t}}\mathrm{\: =\: }277.8\mathit{W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W.r}}$$

$$\mathit{\therefore E_{\mathrm{1}}\mathrm{\: =\: }\mathrm{\frac{1}{2}}\times \frac{V_{m}^{\mathrm{2}}}{\mathrm{\left ( 3600 \right )^{2}}\alpha }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\; \; \mathrm{kWh …(1)}}$$

Energy output to run the train at the speed 𝑽_𝒎 against gradient and resistance to motion (say 𝐸₂) −

$$\mathrm{\mathit{E_{\mathrm{2}}\mathrm{\: =\: }\frac{F_{t}^{'}V_{m}}{\mathrm{3600}}\times \frac{t_{\mathrm{2}}}{\mathrm{3600}}}\; kWh}$$

$$\mathrm{\because Distance\: travelled\: during\: free \: run,\mathit{S^{'}\mathrm{\: =\: }\frac{V_{m}t_{\mathrm{2}}}{\mathrm{3600}}}}$$

$$\mathrm{\therefore \mathit{E_{\mathrm{2}}\mathrm{\: =\: }\frac{F_{t}^{'}\times S'}{\mathrm{3600}}}\;kWh }$$

$$\mathrm{\Rightarrow \mathit{E_{\mathrm{2}}\mathrm{\: =\: }\left [ \mathrm{98.1\, WG\mathrm{\: +\: }W\cdot r} \right ]\times \frac{s'}{\mathrm{3600}}}\; kWh\; \; \cdot \cdot \cdot \left ( 2 \right )}$$

Thus, the total energy output for the run is given by,

$$\mathit{ E\mathrm{\: =\: }\left\{\mathrm{\frac{1}{2}}\times \frac{V_{m}^{\mathrm{2}}}{\mathrm{\left ( 3600 \right )^{2}}\alpha }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'}{\mathrm{3600}}\; \right\}\mathrm{kWh}}$$

$$\mathit{\Rightarrow E\mathrm{\: =\: }\left\{ \frac{V_{m}^{\mathrm{2}}\times \mathrm{1000}}{\mathrm{\mathrm{2}\alpha\left ( 3600 \right )^{2}} }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'\times \mathrm{1000}}{\mathrm{3600}}\; \mathrm{Wh} \right\}}$$

$$\mathit{\Rightarrow E\mathrm{\: =\: }\frac{V_{m}^{\mathrm{2}}}{\mathrm{2}\alpha}\times \frac{\mathrm{1000}}{\mathrm{\left ( 3600 \right )^{2}} }\times \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\frac{V_{m}^{\mathrm{2}}}{\mathrm{2}\alpha}\times \frac{\mathrm{1000}}{\mathrm{\left ( 3600 \right )^{2}} } \left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'\times \mathrm{1000}}{\mathrm{3600}} }$$

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] \left [ \frac{V_{m}^{\mathrm{2}}}{\mathrm{2 \alpha \times 3600}}\mathrm{\: +\: }S^{'} \right ]\times \mathrm{\frac{1000}{3600}}}}$$

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] \left [ S^{"}\mathrm{\: +\: }S^{'} \right ]\times \mathrm{\frac{1000}{3600}}}}$$

Where, 𝑆" is the distance travelled during accelerating period.

Now, if 𝑆₁ = 𝑆" + 𝑆′ is the distance travelled during the acceleration and free run in km. Then, we have,

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\mathrm{0.2778} \left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] S_{\mathrm{1}}}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

Therefore, from the definition of the specific energy output, we get,

$$\mathrm{Specific\: enrgy\: output=\frac{0.01072\, \mathit{V{_{m}}^{\mathrm{2}}W_{e}}+0.2778\left [ 98.1\mathit{WG+W \cdot r} \right ]\times \mathit{S}_{1}}{\mathit{W\times S}}}$$

$$\mathrm{Specific\: enrgy\: output \mathrm{\: =\: } \mathit{\frac{\mathrm{0.01072}V_{m}^{\mathrm{2}}}{S}\times \frac{W_{e}}{W}\mathrm{\: +\: }\mathrm{0.2778}\frac{S_{\mathrm{1}}}{S}\left ( \mathrm{98.1}G\mathrm{\: +\: }r \right )\; \; \cdot \cdot \cdot }\left ( 4 \right )}$$

If the track is level one, i.e., G = 0, then the specific energy output is,

$$\mathrm{Specific\: enrgy\: output \mathrm{\: =\: } \mathit{\frac{\mathrm{0.01072}V_{m}^{\mathrm{2}}}{S}\times \frac{W_{e}}{W}\mathrm{\: +\: }\mathrm{0.2778}\, \frac{S_{\mathrm{1}}}{S}\, r\; \; \cdot \cdot \cdot }\left ( 5 \right )}$$