Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Electric Power and Efficiency of Electric Device
Power or Electric Power
The rate at which work is done in an electric circuit is called as electric power. In other word, the work done per unit time is termed as electric power. It is denoted p or P.
Formula and Unit of Power
When voltage is applied across a resistor, it causes current to flow through it. Therefore, work is being done in moving the electrons through the resistor in a unit time is called the electric power.
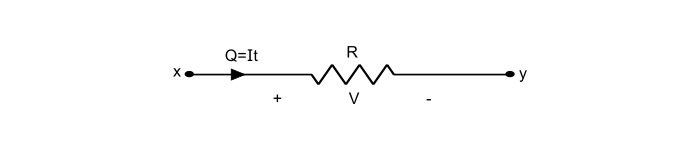
Referring the above figure,
$$\mathrm{V=\frac{work}{Q}}$$
$$\mathrm{\Rightarrow work(W)=VQ=VIt}$$
As, the power is defined as work done per unit time i.e.
$$\mathrm{Power(P)=\frac{work\:done\:in\:electric\:circuit(W)}{Time(t)}=\frac{VIt}{t}}$$
$$\mathrm{(∵V=IR\:or\:I=\frac{V}{R})}$$
$$\mathrm{∴P=VI=I^2R=\frac{V^2}{R}}$$
The above three formulae are equally valid for power calculation. Which one is used depends on the known quantities.
Since, the work done is measure in joules and time in seconds. Therefore, the unit of power is joule/sec or watt i.e.
$$\mathrm{Unit\:of\:Power=\frac{joule}{seconds}=watt}$$
Hence, the power consumed in an electric circuit is 1 watt, if a potential difference of 1 V causes 1 A current to flow through the circuit.
The larger units of power are Kilowatts (kW) Megawatts (MW), and Gigawatts (GW).
$$\mathrm{1\:kW=1000\:W;1MW=10^6\:W=10^3\:kW;1\:GW=10^9W}$$
Sometimes, power is also measured in Horse Power (h.p.),
1 horse power (h.p.) = 746 Watts
Expressions of the power
Expressions of power in the translational system,
$$\mathrm{Power=\frac{Work\:Done}{Time}=\frac{Force×Distance}{Time}=Force×Velocity}$$
Expression of power in the rotational system, If a body makes N r.p.m. and the torque acting on it is τ Newton-meter, then,
$$\mathrm{Work\:done/minute = 2\pi Nτ\:joules}$$
$$\mathrm{Work\:done/sec =\frac{2\pi Nτ}{60}joules/sec}$$
Therefore,
$$\mathrm{Power(P)=\frac{2\pi Nτ}{60}joules/sec\:or\:watts}$$
$$\mathrm{(∵\:746\:watts = 1 h. p. )}$$
$$\mathrm{∴\:Power\:(P)=\frac{2\pi Nτ}{60×746}h.p}$$
Efficiency of Electric Device
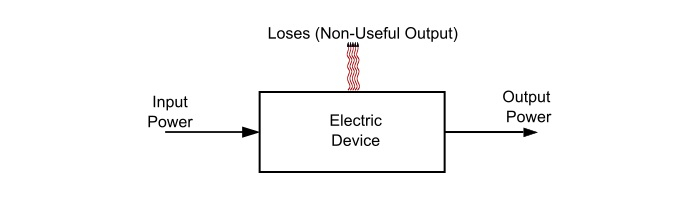
The efficiency of an electric device is defined as the ratio of useful output power to the input power, i.e.,
$$\mathrm{Efficiency(\eta)=\frac{Useful\:Output\:Power(P_{o})}{Input\:Power(P_{i})}}$$
As, the efficiency is the ratio of output and input powers, thus it is a dimensionless quantity. Generally, the efficiency of a device is measured in percentage (%), as,
$$\mathrm{\%\:Efficiency(\eta)=\frac{Useful\:Output\:Power(P_{o})}{Input\:Power(P_{i})} × 100 \%}$$
Some electrical devices have efficiency nearly equal to 100%. An example of such device is electric heater, in which all the input electrical energy is converted into heat energy.
Harmful Effects of Poor Efficiency
The harmful effects of poor efficiency are as follows −
Poor efficiency of the device means greater the losses, thus a large amount of energy is wasted on non-useful output.
The non-useful output appears in the form of heat that raises the temperature of the device. Therefore, poor efficiency means a significant temperature rise. The devices that run hot are more likely to fail.
The heat produced due to poor efficiency has to be dissipated. Thus, the heat removal system increases the cost and size of the device.
Numerical Example - 1
An electric motor is developing a torque of 60 N-m at a speed of 1500 r.p.m. Calculate the power developed by the motor in Watt and h.p.
Solution
$$\mathrm{Power\:developed\:by\:motor,P=\frac{2\pi Nτ}{60}=\frac{2\pi×1500×60}{60}=9420 W}$$
$$\mathrm{(∵\:746\:Watts = 1 h. p. )}$$
$$\mathrm{∴p=\frac{Power\:in\:watts}{746}=\frac{9420}{746}=12.63 h. p.}$$
Numerical Example - 2
A lift of 200 kg mass is raised with a velocity of 10 m/s. if the input power to the driving motor is 21.42 kW. Calculate the % efficiency of the motor.
Solution
Weight of the lift,F = mg = 200 × 9.81 = 1962 Newton
Output power of the motor = Force × Velocity = 1962 × 10 = 19620 W = 19.62 kW
$$\mathrm{\%\:Efficiency=\frac{Output\:power\:of\:motor}{Input\:power\:of\:motor}× 100\:\%\:=\frac{19.62}{21.42}× 100 = 91.59\%}$$
Numerical Example -3
A resistor of 100 Ω has a voltage of 120 V across it. Calculate the power absorbed by the resistor.
Solution
Power abosrbed by resistor,
$$\mathrm{p=\frac{V^2}{R}=\frac{(120)^2}{100}=144 W}$$
768 Views
