
- DIP - Home
- DIP - Image Processing Introduction
- DIP - Signal and System Introduction
- DIP - History of Photography
- DIP - Applications and Usage
- DIP - Concept of Dimensions
- DIP - Image Formation on Camera
- DIP - Camera Mechanism
- DIP - Concept of Pixel
- DIP - Perspective Transformation
- DIP - Concept of Bits Per Pixel
- DIP - Types of Images
- DIP - Color Codes Conversion
- DIP - Grayscale to RGB Conversion
- DIP - Concept of Sampling
- DIP - Pixel Resolution
- DIP - Concept of Zooming
- DIP - Zooming methods
- DIP - Spatial Resolution
- DIP - Pixels Dots and Lines per inch
- DIP - Gray Level Resolution
- DIP - Concept of Quantization
- DIP - ISO Preference curves
- DIP - Concept of Dithering
- DIP - Histograms Introduction
- DIP - Brightness and Contrast
- DIP - Image Transformations
- DIP - Histogram Sliding
- DIP - Histogram Stretching
- DIP - Introduction to Probability
- DIP - Histogram Equalization
- DIP - Gray Level Transformations
- DIP - Concept of convolution
- DIP - Concept of Masks
- DIP - Concept of Blurring
- DIP - Concept of Edge Detection
- DIP - Prewitt Operator
- DIP - Sobel operator
- DIP - Robinson Compass Mask
- DIP - Krisch Compass Mask
- DIP - Laplacian Operator
- DIP - Frequency Domain Analysis
- DIP - Fourier series and Transform
- DIP - Convolution theorm
- DIP - High Pass vs Low Pass Filters
- DIP - Introduction to Color Spaces
- DIP - JPEG compression
- DIP - Optical Character Recognition
- DIP - Computer Vision and Graphics
Digital Image Processing - Introduction to Probability
PMF and CDF both terms belongs to probability and statistics. Now the question that should arise in your mind, is that why are we studying probability. It is because these two concepts of PMF and CDF are going to be used in the next tutorial of Histogram equalization. So if you dont know how to calculate PMF and CDF, you can not apply histogram equalization on your image
.What is PMF?
PMF stands for probability mass function. As it name suggest, it gives the probability of each number in the data set or you can say that it basically gives the count or frequency of each element.
How PMF is Calculated?
We will calculate PMF from two different ways. First from a matrix, because in the next tutorial, we have to calculate the PMF from a matrix, and an image is nothing more then a two dimensional matrix.
Then we will take another example in which we will calculate PMF from the histogram.
Consider this matrix.
| 1 | 2 | 7 | 5 | 6 |
| 7 | 2 | 3 | 4 | 5 |
| 0 | 1 | 5 | 7 | 3 |
| 1 | 2 | 5 | 6 | 7 |
| 6 | 1 | 0 | 3 | 4 |
Now if we were to calculate the PMF of this matrix, here how we are going to do it.
At first, we will take the first value in the matrix , and then we will count, how much time this value appears in the whole matrix. After count they can either be represented in a histogram, or in a table like this below.
PMF
| 0 | 2 | 2/25 |
| 1 | 4 | 4/25 |
| 2 | 3 | 3/25 |
| 3 | 3 | 3/25 |
| 4 | 2 | 2/25 |
| 5 | 4 | 4/25 |
| 6 | 3 | 3/25 |
| 7 | 4 | 4/25 |
Note that the sum of the count must be equal to total number of values.
Calculating PMF from histogram
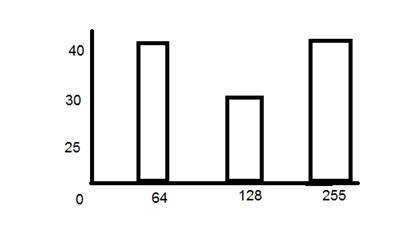
The above histogram shows frequency of gray level values for an 8 bits per pixel image.
Now if we have to calculate its PMF, we will simple look at the count of each bar from vertical axis and then divide it by total count.
So the PMF of the above histogram is this.
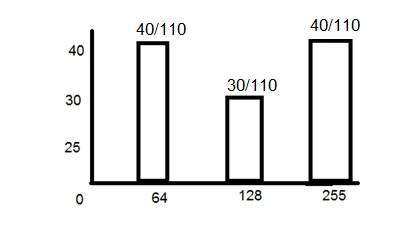
Another important thing to note in the above histogram is that it is not monotonically increasing. So in order to increase it monotonically, we will calculate its CDF.
What is CDF?
CDF stands for cumulative distributive function. It is a function that calculates the cumulative sum of all the values that are calculated by PMF. It basically sums the previous one.
How CDF is Calculated?
We will calculate CDF using a histogram. Here how it is done. Consider the histogram shown above which shows PMF.
Since this histogram is not increasing monotonically, so will make it grow monotonically.
We will simply keep the first value as it is, and then in the 2nd value , we will add the first one and so on.
Here is the CDF of the above PMF function.
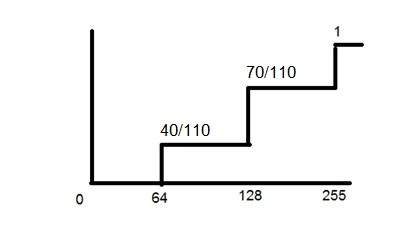
Now as you can see from the graph above, that the first value of PMF remain as it is. The second value of PMF is added in the first value and placed over 128. The third value of PMF is added in the second value of CDF , that gives 110/110 which is equal to 1.
And also now, the function is growing monotonically which is necessary condition for histogram equalization.
PMF and CDF usage in Histogram Equalization
Histogram equalization is discussed in the next tutorial but a brief introduction of histogram equalization is given below.
Histogram equalization is used for enhancing the contrast of the images.
PMF and CDF are both use in histogram equalization as it is described in the beginning of this tutorial. In the histogram equalization, the first and the second step are PMF and CDF. Since in histogram equalization, we have to equalize all the pixel values of an image. So PMF helps us calculating the probability of each pixel value in an image. And CDF gives us the cumulative sum of these values. Further on, this CDF is multiplied by levels, to find the new pixel intensities, which are mapped into old values, and your histogram is equalized.