Image Transformations

---

Before we discuss, what is image transformation, we will discuss what a transformation is.

Transformation

Transformation is a function. A function that maps one set to another set after performing some operations.

Digital Image Processing system

We have already seen in the introductory tutorials that in digital image processing, we will develop a system that whose input would be an image and output would be an image too. And the system would perform some processing on the input image and gives its output as an processed image. It is shown below.

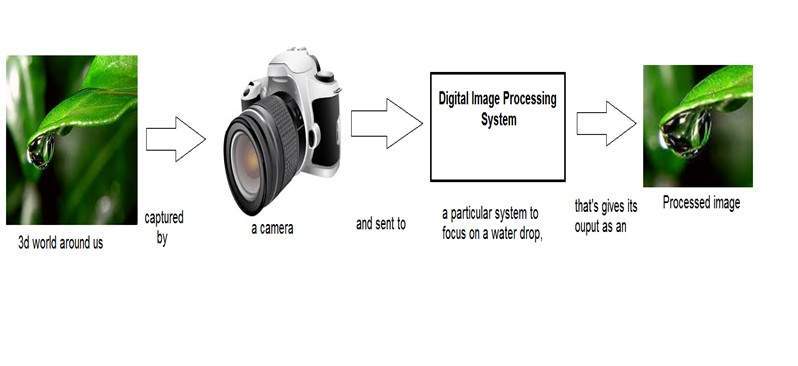
Now function applied inside this digital system that process an image and convert it into output can be called as transformation function.

As it shows transformation or relation, that how an image1 is converted to image2.

Image transformation.

Consider this equation

G(x,y) = T{ f(x,y) }

In this equation,

F(x,y) = input image on which transformation function has to be applied.

G(x,y) = the output image or processed image.

T is the transformation function.

This relation between input image and the processed output image can also be represented as.

s = T (r)

where r is actually the pixel value or gray level intensity of f(x,y) at any point. And s is the pixel value or gray level intensity of g(x,y) at any point.

The basic gray level transformation has been discussed in our tutorial of basic gray level transformations.

Now we are going to discuss some of the very basic transformation functions.

Examples

Consider this transformation function.

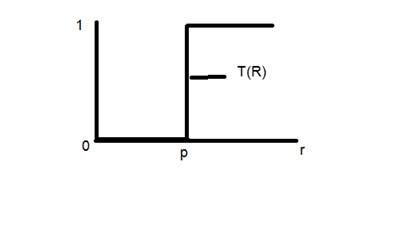
Lets take the point r to be 256, and the point p to be 127. Consider this image to be a one bpp image. That means we have only two levels of intensities that are 0 and 1. So in this case the transformation shown by the graph can be explained as.

All the pixel intensity values that are below 127 (point p) are 0, means black. And all the pixel intensity values that are greater then 127, are 1, that means white. But at the exact point of 127, there is a sudden change in transmission, so we cannot tell that at that exact point, the value would be 0 or 1.

Mathematically this transformation function can be denoted as:

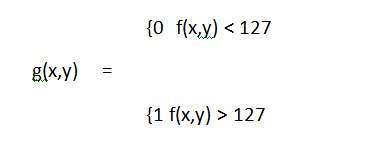
Consider another transformation like this

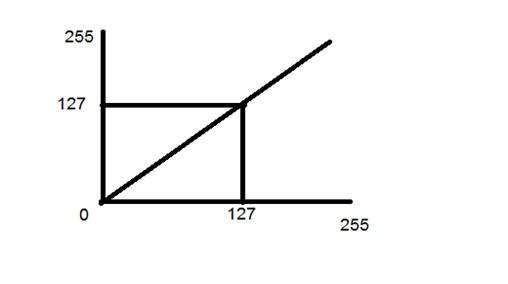
Now if you will look at this particular graph, you will see a straight transition line between input image and output image.

It shows that for each pixel or intensity value of input image, there is a same intensity value of output image. That means the output image is exact replica of the input image.

It can be mathematically represented as:

g(x,y) = f(x,y)

the input and output image would be in this case are shown below.