
- DIP - Home
- DIP - Image Processing Introduction
- DIP - Signal and System Introduction
- DIP - History of Photography
- DIP - Applications and Usage
- DIP - Concept of Dimensions
- DIP - Image Formation on Camera
- DIP - Camera Mechanism
- DIP - Concept of Pixel
- DIP - Perspective Transformation
- DIP - Concept of Bits Per Pixel
- DIP - Types of Images
- DIP - Color Codes Conversion
- DIP - Grayscale to RGB Conversion
- DIP - Concept of Sampling
- DIP - Pixel Resolution
- DIP - Concept of Zooming
- DIP - Zooming methods
- DIP - Spatial Resolution
- DIP - Pixels Dots and Lines per inch
- DIP - Gray Level Resolution
- DIP - Concept of Quantization
- DIP - ISO Preference curves
- DIP - Concept of Dithering
- DIP - Histograms Introduction
- DIP - Brightness and Contrast
- DIP - Image Transformations
- DIP - Histogram Sliding
- DIP - Histogram Stretching
- DIP - Introduction to Probability
- DIP - Histogram Equalization
- DIP - Gray Level Transformations
- DIP - Concept of convolution
- DIP - Concept of Masks
- DIP - Concept of Blurring
- DIP - Concept of Edge Detection
- DIP - Prewitt Operator
- DIP - Sobel operator
- DIP - Robinson Compass Mask
- DIP - Krisch Compass Mask
- DIP - Laplacian Operator
- DIP - Frequency Domain Analysis
- DIP - Fourier series and Transform
- DIP - Convolution theorm
- DIP - High Pass vs Low Pass Filters
- DIP - Introduction to Color Spaces
- DIP - JPEG compression
- DIP - Optical Character Recognition
- DIP - Computer Vision and Graphics
Digital Image Processing - Concept of Sampling
Conversion of Analog Signal to Digital Signal
The output of most of the image sensors is an analog signal, and we can not apply digital processing on it because we can not store it. We can not store it because it requires infinite memory to store a signal that can have infinite values.
So we have to convert an analog signal into a digital signal.
To create an image which is digital, we need to covert continuous data into digital form. There are two steps in which it is done.
- Sampling
- Quantization
We will discuss sampling now, and quantization will be discussed later on but for now on we will discuss just a little about the difference between these two and the need of these two steps.
Basic Idea
The basic idea behind converting an analog signal to its digital signal is

to convert both of its axis (x,y) into a digital format.
Since an image is continuous not just in its co-ordinates (x axis), but also in its amplitude (y axis), so the part that deals with the digitizing of co-ordinates is known as sampling. And the part that deals with digitizing the amplitude is known as quantization.
Sampling
Sampling has already been introduced in our tutorial of introduction to signals and system. But we are going to discuss here more.
Here what we have discussed of the sampling.
The term sampling refers to take samples
We digitize x axis in sampling
It is done on independent variable
In case of equation y = sin(x), it is done on x variable
It is further divided into two parts , up sampling and down sampling
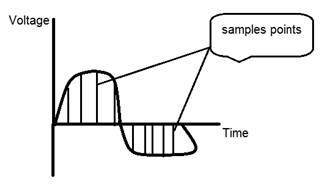
If you will look at the above figure, you will see that there are some random variations in the signal. These variations are due to noise. In sampling we reduce this noise by taking samples. It is obvious that more samples we take, the quality of the image would be more better, the noise would be more removed and same happens vice versa.
However, if you take sampling on the x axis, the signal is not converted to digital format, unless you take sampling of the y-axis too which is known as quantization. The more samples eventually means you are collecting more data, and in case of image, it means more pixels.
Relationship with Pixels
Since a pixel is a smallest element in an image. The total number of pixels in an image can be calculated as
Pixels = total no of rows * total no of columns.
Lets say we have total of 25 pixels, that means we have a square image of 5 X 5. Then as we have dicussed above in sampling, that more samples eventually result in more pixels. So it means that of our continuous signal, we have taken 25 samples on x axis. That refers to 25 pixels of this image.
This leads to another conclusion that since pixel is also the smallest division of a CCD array. So it means it has a relationship with CCD array too, which can be explained as this.
Relationship with CCD array
The number of sensors on a CCD array is directly equal to the number of pixels. And since we have concluded that the number of pixels is directly equal to the number of samples, that means that number sample is directly equal to the number of sensors on CCD array.
Oversampling
In the beginning we have define that sampling is further categorize into two types. Which is up sampling and down sampling. Up sampling is also called as over sampling.
The oversampling has a very deep application in image processing which is known as Zooming.
Zooming
We will formally introduce zooming in the upcoming tutorial, but for now on, we will just briefly explain zooming.
Zooming refers to increase the quantity of pixels, so that when you zoom an image, you will see more detail.
The increase in the quantity of pixels is done through oversampling. The one way to zoom is, or to increase samples, is to zoom optically, through the motor movement of the lens and then capture the image. But we have to do it, once the image has been captured.
Difference between Zooming and Sampling
The concept is same, which is, to increase samples. But the key difference is that while sampling is done on the signals, zooming is done on the digital image.