Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct Tree from given Inorder and Preorder traversals in C++
We are given the Inorder and Preorder traversals of a binary tree. The goal is to construct a tree from given traversals.
Inorder traversal − In this type of tree traversal, a left subtree is visited first, followed by the node and right subtree in the end.
Inorder (tree root)
Traverse left subtree of node pointed by root, call inorder ( root→left )
Visit the root
Traverse right subtree of node pointed by root, call inorder ( root→right )
Preorder traversal − In this type of tree traversal, the node visited first, followed by the left subtree and right subtree in the end.
Preorder (tree root)
- Visit the root
- Traverse left subtree of node pointed by root, call inorder ( root→left )
- Traverse right subtree of node pointed by root, call inorder ( root→right )
The inorder and preorder traversal of below tree are given −
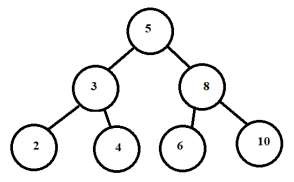
Inorder
2-3-4-5-6-8-10
Preorder
4-3-2-5-8-6-10
Now we’ll construct the above tree again for given preorder and inorder traversals.
Inorder
2-3-4-5-6-8-10
Preorder
5-3-2-4-8-6-10
As we know that preorder visits the root node first then the first value always represents the root of the tree. From above sequence 5 is the root of the tree.
Preorder
5 -3-2-4-8-6-10
From above inorder traversal, we know that a node’s left subtree is traversed before it followed by its right subtree. Therefore, all values to the left of 5 in inorder belong to its left subtree and all values to the right belong to its right subtree.
Inorder
2-3-4 ← 5 → 6-8-10
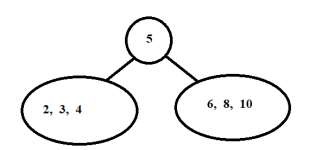
- Now for the left subtree do the same as above.
Preorder traversal of left subtree is 3 -2-4. So 3 becomes the root.
Inorder traversal divided further into 2 ← 3 → 4
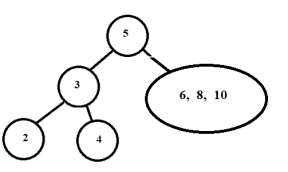
- Now for the right subtree do the same as above.
Preorder traversal of the right subtree is 8 -6-10. So 8 becomes the root.
Inorder traversal divided further into 6 ← 8 → 10
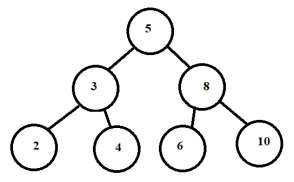
So, in this way we constructed the original tree from given preorder and inorder traversals.
733 Views
