Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct Special Binary Tree from given Inorder traversal in C++
We are given an array arr[] containing the inorder traversal of a binary tree. The goal is to construct a special binary tree from that array. A special binary tree is the one which has root node’s weight greater than the weights of both its left and right children.
For Example
Input
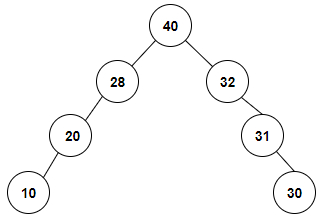
int arr[] = {10, 20, 28, 40, 32, 31, 30}Output
The special binary tree which will be constructed with the given inorder traversal is given below −
Explanation
we are given with an array of integer values or the inorder traversal of a tree. So, the special tree formed is 10, 20, 28, 40, 32, 31, 30
Input
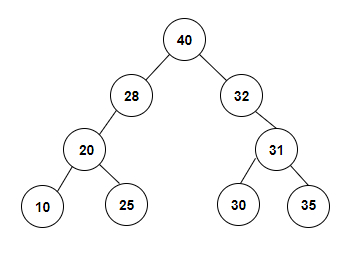
int arr[] = {10, 20, 25, 28, 40, 32, 31, 30, 35}Output
The special binary tree which will be constructed with the given inorder traversal is given below −
Explanation
we are given with an array of integer values or the inorder traversal of a tree. So, the special tree formed is 10, 20, 25, 28, 40, 32, 31, 30, 35.
Approach used in the below program is as follows −
In this approach we will construct the special binary tree from the given array taking the maximum element as the root node. The left elements to that will become part of left subtree and right elements to that will become part of right subtree. This process is recursively done to construct the tree.
Take arr[] as an input array containing the inorder traversal.
Function new_node (int data) creates a node with left and right children as NULL.
Function total(int arr[], int first, int last) returns the index of that element.
Take highest = arr[first] and lowest = first.
Traverse from the first+1 index till the last and if any element arr[i] is found more than highest then store its index in lowest and update highest.
At the end of for loop lowest will contain the index of highest element.
Function create_tree (int arr[], int first, int last) constructs the special binary tree from arr[] recursively.
If first>last then return NULL as the tree won't be possible.
Take temp as the maximum value of the array using temp = total(arr, first, last).
Create a node with temp as data and make a pointer parent point to it for root node of the tree.
If first==last then the tree would have only one node. Return parent.
Recursively calculate parent->left = create_tree(arr, first, temp − 1);
And parent−>right = create_tree(arr, temp + 1, last).
At the end return the parent.
Function Inorder_traversal(tree_node* node) prints the inorder traversal of the tree generated above.
If the node is NULL then return nothing. Else print left subtree first using Inorder_traversal(node−>left).
Then print the current node.
Then print the right subtree using Inorder_traversal (node−>right).
Example
#include <bits/stdc++.h>
using namespace std;
int total(int arr[], int first, int last);
class tree_node{
public:
int data;
tree_node* left;
tree_node* right;
};
tree_node* new_node(int data);
tree_node* create_tree (int arr[], int first, int last){
if(first > last){
return NULL;
}
int temp = total(arr, first, last);
tree_node *parent = new_node(arr[temp]);
if(first == last){
return parent;
}
parent−>left = create_tree(arr, first, temp − 1);
parent−>right = create_tree(arr, temp + 1, last);
return parent;
}
int total(int arr[], int first, int last){
int highest = arr[first];
int lowest = first;
for(int i = first + 1; i <= last; i++){
if(arr[i] > highest){
highest = arr[i];
lowest = i;
}
}
return lowest;
}
tree_node* new_node (int data){
tree_node* newNode = new tree_node();
newNode−>data = data;
newNode−>left = NULL;
newNode−>right = NULL;
return newNode;
}
void Inorder_traversal(tree_node* node){
if (node == NULL){
return;
}
Inorder_traversal(node−>left);
cout<<node−>data<<" ";
Inorder_traversal (node−>right);
}
int main(){
int arr[] = {10, 20, 28, 40, 32, 31, 30};
int size = sizeof(arr)/sizeof(arr[0]);
tree_node *root = create_tree(arr, 0, size − 1);
cout<<"Construct Special Binary Tree from given Inorder traversal are: "<<"\n";
Inorder_traversal(root);
return 0;
}Output
If we run the above code it will generate the following output −
Construct Special Binary Tree from given Inorder traversal are: 10, 20, 28, 40, 32, 31, 30
296 Views
