Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct Binary Tree from String in C++
Suppose we have a string consisting of parenthesis and integers. We have to construct a binary tree from that string. The whole input represents a binary tree. It holds an integer that followed by zero, one or two pairs of parentheses. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
So, if the input is like "4(2(3)(1))(6(5))", then the output will be [3,2,1,4,5,6] (inorder traversal)
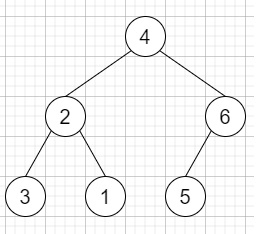
To solve this, we will follow these steps −
Define a function solve(), this will take s, idx,
if idx >= size of s, then −
return null
num := empty string
while (idx < size of s and s[idx] is not equal to '(' and s[idx] is not equal to ')'), do −
num := num + s[idx]
(increase idx by 1)
node = new node with value num
if idx < size of s and s[idx] is same as '(', then −
(increase idx by 1)
left of node := solve(s, idx)
(increase idx by 1)
if idx < size of s and s[idx] is same as '(', then −
(increase idx by 1)
right of node := solve(s, idx)
(increase idx by 1)
return node
From the main method do the following −
idx := 0
temp = new node with value -1
return solve(s, idx)
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void inord(TreeNode *root){
if(root != NULL){
inord(root->left);
cout << root->val << " ";
inord(root->right);
}
}
class Solution {
public:
TreeNode* solve(string s, int& idx){
if (idx >= s.size())
return NULL;
string num = "";
while (idx < s.size() && s[idx] != '(' && s[idx] != ')') {
num += s[idx];
idx++;
}
TreeNode* node = new TreeNode(stoi(num));
if (idx < s.size() && s[idx] == '(') {
idx++;
node->left = solve(s, idx);
idx++;
if (idx < s.size() && s[idx] == '(') {
idx++;
node->right = solve(s, idx);
idx++;
}
}
return node;
}
TreeNode* str2tree(string s) {
int idx = 0;
TreeNode* temp = new TreeNode(-1);
return solve(s, idx);
}
};
main(){
Solution ob;
TreeNode *root = ob.str2tree("4(2(3)(1))(6(5))");
inord(root);
}Input
"4(2(3)(1))(6(5))"
Output
3 2 1 4 5 6
1K+ Views
