Recover a Tree From Preorder Traversal in C++

Suppose there is a binary tree. We will run a preorder depth first search on the root of a binary tree.

At each node in this traversal, the output will be D number of dashes (Here D is the depth of this node), after that we display the value of this node. As we know if the depth of a node is D, the depth of its immediate child is D+1 and the depth of the root node is 0.

Another thing we have to keep in mind that if a node has only one child, that child is guaranteed to be the left child. So, if the output S of this traversal is given, then recover the tree and return its root.

So, if the input is like "1-2--3--4-5--6--7", then the output will be

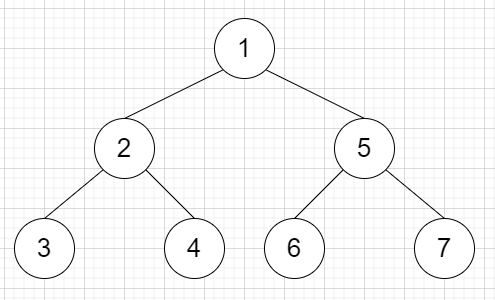
To solve this, we will follow these steps −

• Define one stack st

• i := 0, n := size of S

• lvl := 0, num := 0

• while i < n, do −

  • for initialize lvl := 0, when S[i] is same as '-', update (increase lvl by 1), (increase i by 1), do −

    • do nothing

  • num := 0

  • while (i < n and S[i] is not equal to '-'), do −

    • num := num * 10 + (S[i] - '0')

    • (increase i by 1)

  • while size of st > lvl, do −

    • delete element from st

  • temp = create a new Tree Node with num value

  • if not st is empty and not left of top element of st is null, then −

    • left of top element of st := temp

  • otherwise when not st is empty, then −

    • right of top element of st := temp

  • insert temp into st

• while size of st > 1, do −

  • delete element from st

• return (if st is empty, then NULL, otherwise top element of st)

Let us see the following implementation to get better understanding −

Example

 Live Demo

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = NULL;
      right = NULL;
   }
};
void inord(TreeNode *root){
   if(root != NULL){
      inord(root->left);
      cout << root->val << " ";
      inord(root->right);
   }
}
class Solution {
   public:
   TreeNode* recoverFromPreorder(string S) {
      stack<TreeNode*> st;
      int i = 0;
      int n = S.size();
      int lvl = 0;
      int num = 0;
      while (i < n) {
         for (lvl = 0; S[i] == '-'; lvl++, i++)
         ;
         num = 0;
         while (i < n && S[i] != '-') {
            num = num * 10 + (S[i] - '0');
            i++;
         }
         while (st.size() > lvl)
         st.pop();
         TreeNode* temp = new TreeNode(num);
         if (!st.empty() && !st.top()->left) {
            st.top()->left = temp;
         }
         else if (!st.empty()) {
            st.top()->right = temp;
         }
         st.push(temp);
      }
      while (st.size() > 1)
      st.pop();
      return st.empty() ? NULL : st.top();
   }
};
main(){
   Solution ob;
   TreeNode *root = ob.recoverFromPreorder("1-2--3--4-5--6--7");
   inord(root);
}

Input

"1-2--3--4-5--6--7"

Output

3 2 4 1 6 5 7