Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct the SLR Parsing table for the following grammar. Also, Parse the input string a * b + a.
Description − Consider the Grammar
E → E + T|T
T → TF|F
F → F*|a|b.
Solution
Step1 − Construct the augmented grammar and number the productions.
(0) E′ → E
(1) E → E + T
(2) E → T
(3) T → TF
(4) T → F
(5) F → F ∗
(6) F → a
(7) F → b.
Step2 − Find closure & goto Functions to construct LR (0) items.
Box represents the New states, and the circle represents the Repeating State.
Computation of FOLLOW
We can find out
FOLLOW(E) = {+, $}
FOLLOW(T) = {+, a, b, $}
FOLLOW(F) = {+,*, a, b, $}
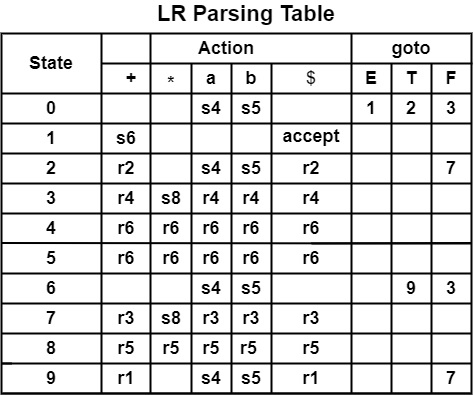
Parsing for Input String a * b + a −
| Stack | Input String | Action |
|---|---|---|
| 0 | a * b + a $ | Shift |
| 0 a 4 | * b + a $ | Reduce by F → a. |
| 0 F 3 | * b + a $ | Shift |
| 0 F 3 * 8 | b + a $ | Reduce by F → F ∗ |
| 0 F 3 | b + a $ | Reduce by T → F |
| 0 T 2 | b + a $ | Shift |
| 0 T 2 b 5 | +a $ | Reduce by F → b |
| 0 T 2 F 7 | +a $ | Reduce by T → TF |
| 0 T 2 | +a $ | Reduce by E → T |
| 0 E 1 | +a $ | Shift |
| 0 E 1 + 6 | a$ | Shift |
| 0 E 1 + 6 a 4 | $ | Reduce by F → a |
| 0 E 1 + 6 F 3 | $ | Reduce by T → F |
| 0 E 1 + 6 T 9 | $ | Reduce by E → E + T |
| 0 E 1 | $ | Accept |
Updated on: 02-Nov-2021
31K+ Views
Advertisements