Construct SLR (1) parsing table for the grammar\\n1. E → E + T\\n2. E → T\\n3. T → T * F\\n4. T → F\\n5.F → (E)\\n6.F → id

Solution

Steps to produce SLR Parsing Table

• Generate Canonical set of LR (0) items

• Compute FOLLOW as required by Rule (2b) of Parsing Table Algorithm.

Computation of FOLLOW

By Rule (1) of FOLLOW

FOLLOW(E) = {$}                                                   (1)

• E → E + T

Applying Rule (2) FOLLOW

i.e., comparing E → E + T with A → α B β

E →	Ε	E	+ T
A →	Α	B	Β

∴ A = E, α = ε, B = E, β = +T

? Since FIRST(β) = FIRST(+T) = {+}which does not contain ε.

∴ Rule (2b)of FOLLOW

FOLLOW(E) = {+}                                                    (2)

Applying Rule (3) of FOLLOW

E →	Ε +	T
A →	α	B

FOLLOW(T) = {FOLLOW(E)}                                   (3)

• E → T

Rule (2) cannot be applied. As E → T cannot be compared with A → α B β. Applying Rule (3) of FOLLOW

E →	ε	T
A →	α	B

FOLLOW(T) = {FOLLOW(E)}                                  (4)

• T → T* F

Applying Rule (2) of FOLLOW

T →	E	T	*F
A →	A	B	β

∴ FIRST(β) = FIRST(∗ F) = {*}

Rule (2a)

∴ FOLLOW (T) = {*}                                                (5)

Applying Rule (3) FOLLOW

T →	T*	F
A →	α	B

∴ FOLLOW (F) = {FOLLOW(T)}                                (6)

• T → F

Rule (2) cannot be applied. As T → F cannot be compared with A → α B β

Applying Rule (3)

T →	ε	F
A →	α	B

FOLLOW (F) = {FOLLOW(T)} (7)

• F → (E)

Applying Rule (2) FOLLOW

A →	(	E	)
F →	A	B	β

∴ FIRST(β) = FIRST()) = { )}

FOLLOW(E) = { )} (8)

Rule (3) cannot be applied.

• F → id

Rule (2) and (3), both cannot be applied to this production. As they cannot be compared with F → id.

Combining (1) to (8)

FOLLOW(E) = {$}                                            (1)

FOLLOW(E) = {+}                                            (2)

FOLLOW(T) = {FOLLOW(E)}                          (3)

FOLLOW(T) = {FOLLOW(E)}                          (4)

FOLLOW (T) = {*}                                            (5)

FOLLOW (F) = {FOLLOW(T)}                          (6)

FOLLOW (F) = {FOLLOW(T)}                          (7)

FOLLOW(E) = { )}                                            (8)

∴ From (1), (2)and (8)

FOLLOW(E) = {$, +, )}

From (3), (4), (5), (8)

FOLLOW(T) = {$, +, ),*}

From (6) and (7)

FOLLOW(F) = {$, +, ) *}

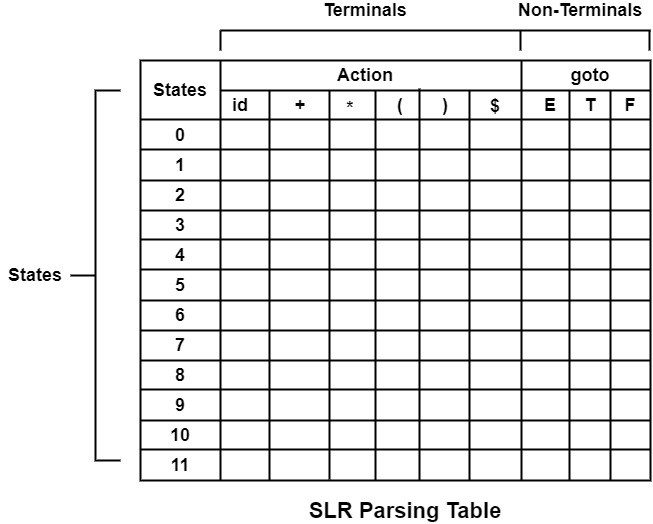
Construct the structure of a table in the following way −

• Write down all states I₀ to I₁₁(i. e. , 0 to 11) Row-wise.
• Write down the terminal symbols in Action column-wise.
• Write down the non-terminals column-wise in goto column-wise.