Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Consider the ambiguous grammar.
E β E + E
E β E * E
E β (E)
E β id
(a) Construct LR (0) items for above grammar.
(b) Construct SLR parsing table for grammar.
(c) Parse the input string id + id * id.
Solution
Step1− Construct Augmented Grammar
(0) E′ → S
(1) E → E + E
(2) E → E ∗ E
(3) E → (E)
(4) E → id
Step2− Find closure & goto functions to construct LR (0) items.
Closure (E′ → β E) =
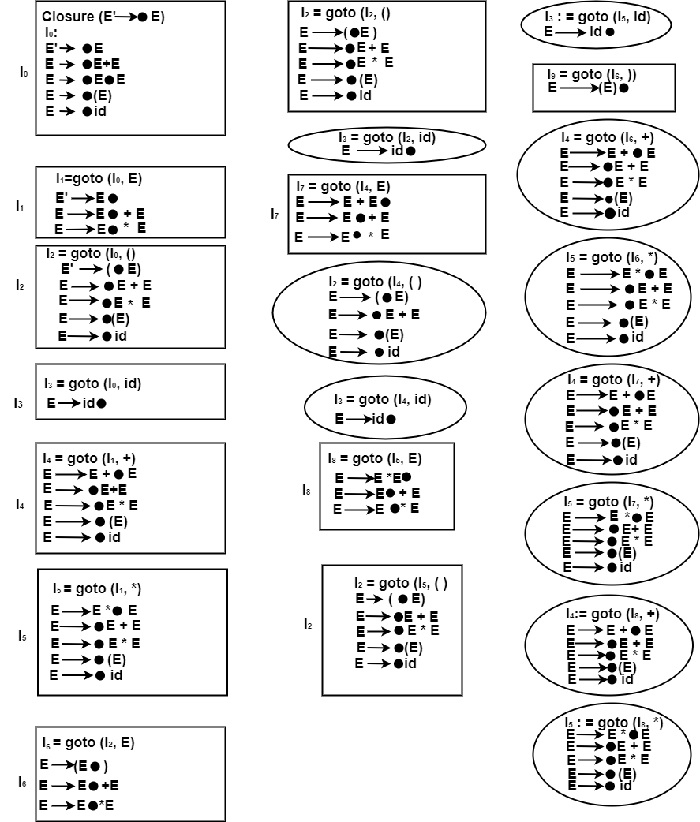
Applying goto on I9
β΅ goto cannot be applied on I9, as the dot in E → (E). is on the last position.
Step3− Computation of FOLLOW
Applying Rule (1) FOLLOW
FOLLOW(B) = {$} (1)
- E → E + E
Comparing E → E + E with A → α B β
∴ α = ε, B = E, β = +E
β΅ FIRST(β) = FIRST(+E) = {+}
∴ Rule (2a)of FOLLOW
FOLLOW(E) = {+} (2)
Applying Rule (3)
Comparing E → E + E with A → α B
∴ A = E, α = E+, B = E
FOLLOW(E) = {FOLLOW(E)} (3)
- E → E ∗ E
Applying Rule (2) and Rule (3) of FOLLOW, we get
FOLLOW(E) = {*} (4)
FOLLOW(E) = {FOLLOW(E)} (5)
- E → (E)
Applying Rule (2)
Comparing E → (E) with A → α B β
∴ FOLLOW (E) = {)} (6)
Rule (3) cannot be applied to this production
As E → (E) cannot be compared with A → α B
- E → id
Rule (2) and (3) of FOLLOW cannot be applied on E → id. As E → id cannot be compared with A → α B β and A → α B.
Combining (1) to (6), we get
FOLLOW (E) = {$, +,*, )}
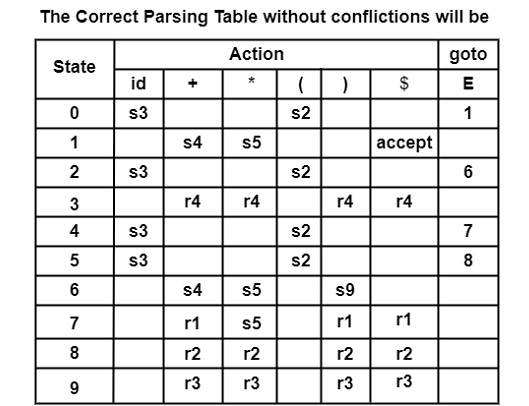
Step4 − Construction of SLR Parsing Table
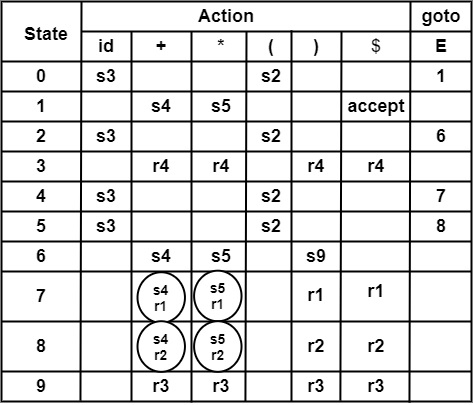
In the parsing table, conflict occurs at Row state 7, 8, and column *, +.
In Action [7, +], Action [7, *]
Action [8, +], Action [8, *] there occurs a shift-reduce conflict.
The Association and precedence rules can remove this conflict.
Parsing the string id + id * id
| Stack | Input | Action |
|---|---|---|
| 0 | id + id * id $ | Shift |
| 0 id 3 | + id * id $ | Reduce by E → id |
| 0 E 1 | +id * id $ | Shift |
| 0 E 1 + 4 | id * id $ | Shift |
| 0 E 1 + 4 id 3 | * id $ | Reduce by E → id |
| 0 E 1 + 4 E 7 | * id $ | Conflict i. e. , s5 or r1 ∴ * has higher precedence then + ∴ Action [7,∗] = s5 So, shift-reduce, i.e., s5 |
| 0 E 1 + 4 E 7 * 5 | $ | Shift |
| 0 E 1 + 4 E 7 * 5 id 3 | $ | Reduce by E → id |
| 0 E 1 + 4 E 7 * 5 E 8 | $ | Reduce by E → E * E |
| 0 E 1 + 4 E 7 | $ | Reduce by E → E + E |
| 0 E 1 | $ | accept |
The above parsing solves the conflicting problem in Action [7, *].
So, Action [7, *] = s5 instead of r1.
Similarly on Parsing the string id + id + id.
| Stack | Input | Action |
|---|---|---|
| 0 | id + id + id $ | Shift |
| 0 id 3 | + id + id $ | Reduce by E → id |
| 0 E 1 | +id + id $ | Shift |
| 0 E 1 + 4 | id + id $ | Shift |
| 0 E 1 + 4 id 3 | +id $ | Reduce by E → id |
| 0 E 1 + 4 E 7 | +id $ | Conflict i. e. , Action [7, +] = s4 or r1. ∴ + is Associative (left). 0E1 + 4E7 will be reduced before shifting + ∴ Action [7, +] = r1 ∴ Reduce by E → E + E |
| 0 E 1 | +id $ | Shift |
| 0 E + 4 | id $ | Shift |
| 0 E + 4 id 3 | $ | Reduce by E → id |
| 0 E + 4 E 7 | $ | Reduce by E → E + E |
| 0 E 1 | $ | accept |
So, the Above parsing shows how to resolve shift Reduce conflict at Action [7, +]
So, Action [7, +] = r1 instead of s4
Similarly, other entries such as Action [8, +] and Action [8, *] can be solved by taking strings.
id * id * id and id * id + id
Resolution is Action [8, +] = r2 and
Action [8, *] = r2.
3K+ Views
