Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct Pushdown automata for L = {a(2*m)c(4*n)dnbm | m,n = 0} in C++
We are given with a language “L” and the task is to construct a pushdown automata for the given language which explains that the occurrences of character ‘a’ should be doubles the time of occurrence of character ‘b’ and occurrences of character ‘c’ should be quadruples the times of ‘d’ and also occurrences of all the characters should be minimum 1 which can also makes the string NULL and it should be accepted by the automata.
What is pushdown Automata?
A pushdown automata or pushdown automaton or PDA is a technique to implement a context-free grammar in a similar way we design Deterministic Finite Automaton or DFA for a regular grammar. A DFA can operate on finite data, but a PDA can operate on infinite data. We can understand pushdown automata as the combination of “finite state machine” and a “stack”.
A pushdown automaton has three components −
an input tape,
a control unit, and
a stack with infinite size.
A PDA can be formally described as a 7−tuple (Q, Σ, S, δ, q0, I, F) −
Q is the finite number of states
Σ is input alphabet
S is stack symbols
δ is the transition function: Q × (Σ υ {ε}) × S × Q × S*
q0 is the initial state (q0 Ε Q)
I is the initial stack top symbol (I Ε S)
F is a set of accepting states (F Ε Q)
Let’s construct a pushdown Automata for the given language −
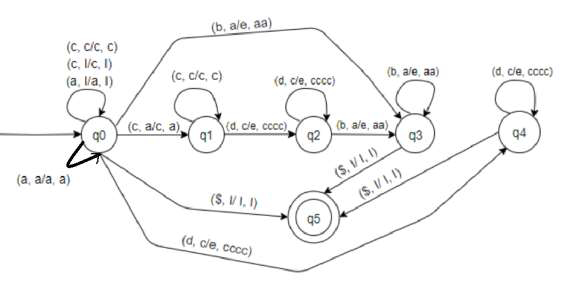
The strings that are acceptable by this PDA are of the form −
c4ndn − ccccd, ccccccccdd, etc. No. of cs is 4 times the no. of ds. When m is 0 we will have no as and bs. Keep pushing cs and as soon as the first d is encountered then pop 4 c from stack. If we reach the end of the string and are left with no cs then the string is accepted.
a2mbm − aab, aaaabb, etc. No. of as is 2 times the no. of bs. When n is 0 we will have no cs and ds. Keep pushing as and as soon as the first b is encountered then pop 2 b from stack. If we reach the end of the string and are left with no as then the string is accepted.
a2mc4ndnbm − aaccccdb, aaaaccccccccddbb. No. of as is 2 times the no. of bs and cs equal to 4 times the number of ds. Keep pushing as and cs. As soon as the first d is encountered then pop 4 cs if it's on top and then pop 2 as for the rest of bs. If we reach the end and no a is left then the string is accepted.
NULL string is also accepted. a0c0d0b0.
Let’s understand the machine
Transitions for state q0 −
( a, I/a,I ) − If top of stack is I and current input symbol is a then push a to top of stack and remain at q0. Stack becomes aI…
( c, I/c,I ) − If top of stack is I and current input symbol is c then push c to top of stack and remain at q0. Stack becomes cI...
( a, a/a,a ) − If top of stack is a and current input symbol is also a then push a to top of stack and remain at q0. Stack becomes aa.... Keep pushing as until the next c or b.
( c, c/c,c ) − If top of stack is c and current input symbol is also c then push c to top of stack and remain at q0. Stack becomes cc.... Keep pushing cs until the next d.
( b, a/e,aa ) − If top of stack is a and current input symbol is b then pop 2 as from stack and move to q3.
(c, a/c,a ) − If top of stack is a and current input symbol is c then push c to top of stack and move to q1. Stack becomes ca...
( d, c/e,cccc ) − If top of stack is c and current input symbol is d then pop 4 ds from stack and move to q4.
( $, I/I, I) − If top of stack is I and there is no input then do nothing and move to q5. For NULL string.
Transitions for state q1 −
( c, c/c,c ) − If top of stack is c and current input symbol is also c then push c to top of stack and remain at q1. Stack becomes cc.... Keep pushing cs until the next d.
( d, c/e,cccc ) − If top of stack is c and current input symbol is d then pop 4 ds from stack and move to q2.
Transitions for state q2 −
( d, c/e,cccc ) − If top of stack is c and current input symbol is d then pop 4 ds from stack and move to q2.
( b, a/e,aa ) − If top of stack is a and current input symbol is b then pop 2 as from stack and move to q3.
Transitions for state q3 −
( b, a/e,aa ) − If top of stack is a and current input symbol is b then pop 2 as from stack and remain at q3.
( $, I/I, I ) − If top of stack is I and there is no input then do nothing and move to q5. For NULL string.
Transitions for state q4 −
( d, c/e,cccc ) − If top of stack is c and current input symbol is d then pop 4 ds from stack and remain at q4.
( $, I/I, I ) − If top of stack is I and there is no input then do nothing and move to q5. For NULL string.
384 Views
To Continue Learning Please Login