Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct DPDA for a(n+m)bmcn n,m≥1 in TOC
A push down automata (PDA) can be formally described as seven tuples
(Q, Σ,S, δ,q0,I,F)
Where,
- Q is finite number of states
- Σ is input alphabet
- S is stack symbol
- Δ is the transition function: QX(Σ∪{e})XSXQ
- q0 is the initial state (q0 belongs to Q)
- I is the initial state top symbol
- F is a set of accepting states
Problem
Construct PDA for a(n+m)bmcn n,m≥1.
Solution
So, the strings which are generated by the given language are −
L={aabc,aaaabccc,aaaaabbccc,….}
That is to add the number of b's and c's, and that will equal the number of a's.
For every b's and c's we will pop a's from the stack.
Let’s count the number of a's and that is equal to the sum of b's and c's.
It can be achieved by pushing a's in stack and then we will pop a's whenever "b" or"c" comes.
Finally, at the end of the strings if nothing is left in the STACK then we can say that language is accepted in the PDA.
The PDA for given problem is as follows −
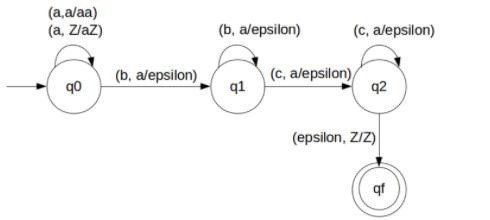
Transition functions
The transition functions are as follows −
Step 1: δ(q0, a, Z) = (q0, aZ)
Step 2: δ(q0, a, a) = (q0, aa)
Step 3: δ(q0, b, a) = (q1, ε)
Step 4: δ(q1, b, a) = (q1, ε)
Step 5: δ(q1, c, a) = (q2, ε)
Step 6: δ(q2, c, a) = (q2, ε)
Step 7: δ(q2, ε, Z) = (qf, Z)
Explanation
Step 1 − Let’s take an input string: "aaaabbcc" which satisfies the given condition.
Step 2 − Scan string from left to right.
Step 3 − For input 'a' and STACK alphabet Z, then
Push the input 'a' into STACK: (a,Z/aZ) and state will be q0
Step 4 − For input 'a' and STACK alphabet 'a', then
Push the input 'a' into STACK: (a,a/aa) and state will be q0
Step 5 − For input 'a' and STACK alphabet 'a', then
Push the input 'a' into STACK: (a,a/aa) and state will be q0
Step 6 − For input 'a' and STACK alphabet 'a', then
Push the input 'a' into STACK: (a,a/aa) and state will be q0
Step 7 − For input 'b' and STACK alphabet 'a' and state is q0, then
Pop one 'a': (c,a/ε) and state will be q1
Step 8 − For input 'b' and STACK alphabet 'a' and state is q1, then
Pop one 'a': (c,a/ε) and state remain q1
Step 9 − For input 'c' and STACK alphabet 'a' and state is q1, then
Pop one 'a': (c,a/ε) and state will be q2
Step 10 − For input 'c' and STACK alphabet 'a' and state is q2, then
Pop one 'a': (c,a/ε) and state will be remain q2
Step 11 − We reached end of the string, on input ε and STACK alphabet Z, then
Go to final state(qf): (ε, Z/Z)
762 Views
