
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct DFA with Σ= {0,1} accepts all strings with 0.
A Deterministic Finite automata (DFA) is a collection of defined as a 5-tuples and is as follows −
M=(Q, Σ, δ,q0,F)
Where,
- Q: Finite set called states.
- Σ: Finite set called alphabets.
- δ: Q × Σ → Q is the transition function.
- q0 ∈ Q is the start or initial state.
- F: Final or accept state.
Example 1
The DFA accepts all strings starting with 0
The language L= {0,01,001,010,0010,000101,…}
In this language, all strings start with zero.
Transition diagram
The transition diagram is as follows −
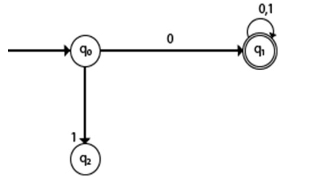
Explanation
- Step 1 − q0 is the initial state on input ‘0’ it goes to q1, which is the final state, and ‘0’ string is accepted.
- Step 2 − q0 on ‘1’ goes to q2 which is dead state because for q2 there is no path to reach to the final state.
- Step 3 − q1 on input ‘0’ and ‘1’ goes to q1 itself which is the final state.
Transition table
The transition table is as follows −
| State/input symbol | 0 | 1 |
|---|---|---|
| ->q0 | q1 | q2 |
| q1 | q1 | q1 |
| q2 | - | - |
Example 2
Construct DFA for the language accepting strings starting with ‘101’
- All strings start with substring “101”.
- Then the length of the substring = 3.
Therefore, Minimum number of states in the DFA = 3 + 2 = 5.
The minimized DFA has five states.
The language L= {101,1011,10110,101101,.........}
The transition diagram is as follows −
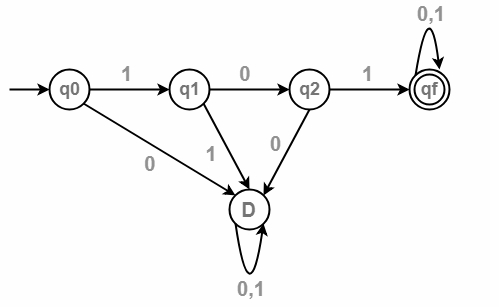
Explanation
- Step 1 − q0 is an initial state on input ‘1’ goes to q1 and on input ‘0’ leads to a dead state.
- Step 2 − q1 on input ‘0’ goes to q2 and on ‘1’ goes to dead state.
- Step 3 − q2 on input ‘1’ goes to qf which is the final state, and on ‘0’ goes to dead state.
- Step 4 − qf is the final state, on input ‘1’ and ‘0’ it goes to qf itself.

Advertisements
